1. Метод прогонки решения СЛАУ, условие применимости.




Условия применимости метода прогонки
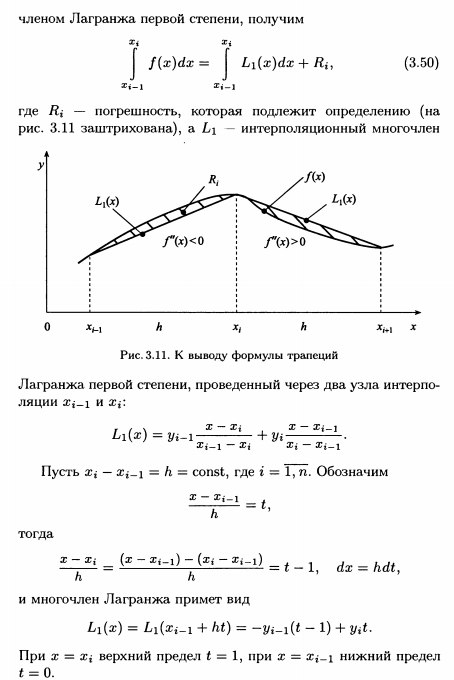
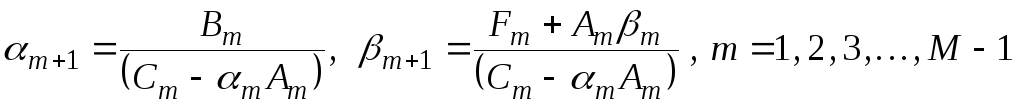 (3.3.9)
(3.3.9)
В процессе вычисления величин 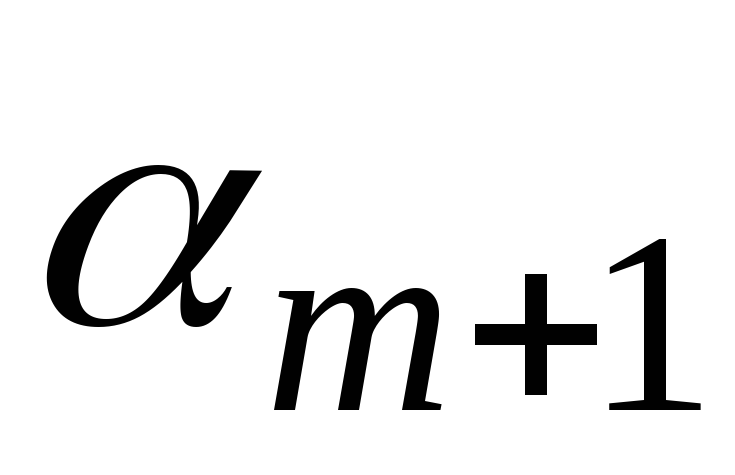 и
и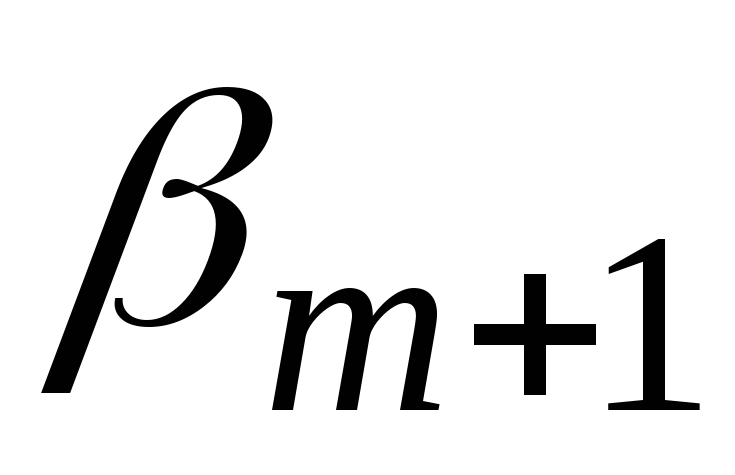 по формулам (3.3.9) происходит деление на величины
по формулам (3.3.9) происходит деление на величины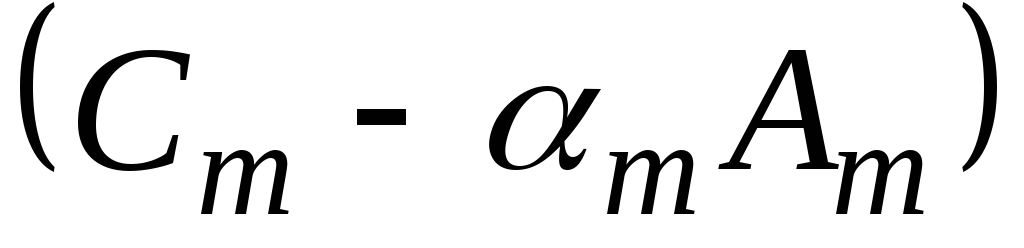 , которые могут обращаться в ноль. В этом случае метод прогонки применять нельзя. Поэтому необходимо знать и предварительно проверять условия, при которых можно использовать этот метод. Достаточные условия применимости метода прогонки сформулируем в виде теоремы.
, которые могут обращаться в ноль. В этом случае метод прогонки применять нельзя. Поэтому необходимо знать и предварительно проверять условия, при которых можно использовать этот метод. Достаточные условия применимости метода прогонки сформулируем в виде теоремы.
Теорема 1. Если
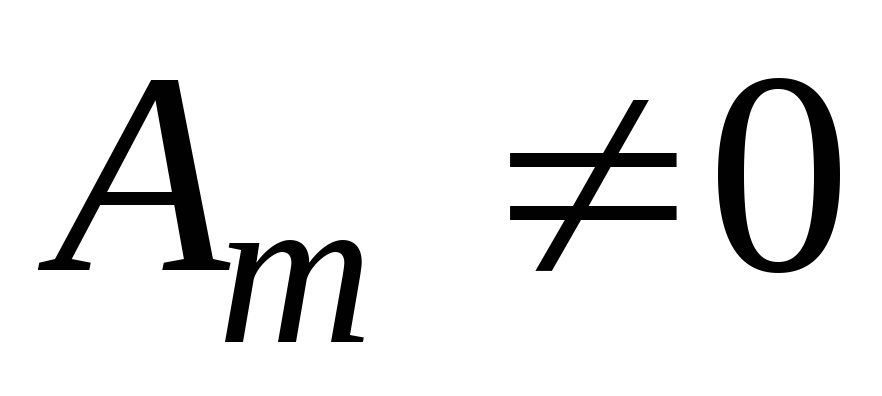 ,
, 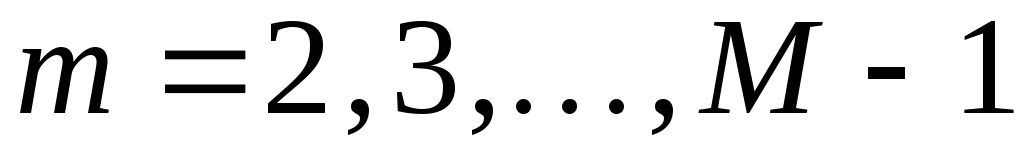 ,
,
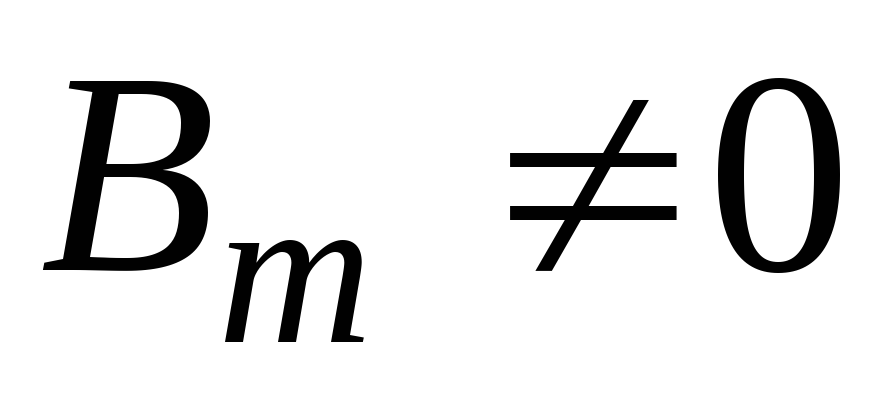 ,
,  ,
,
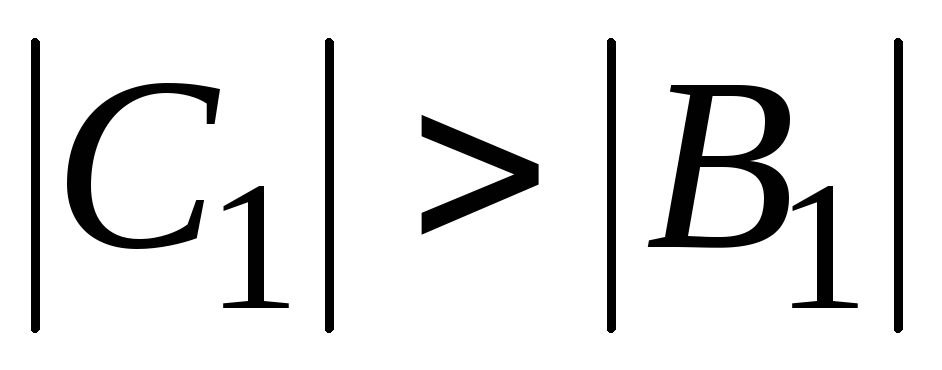 ,
, 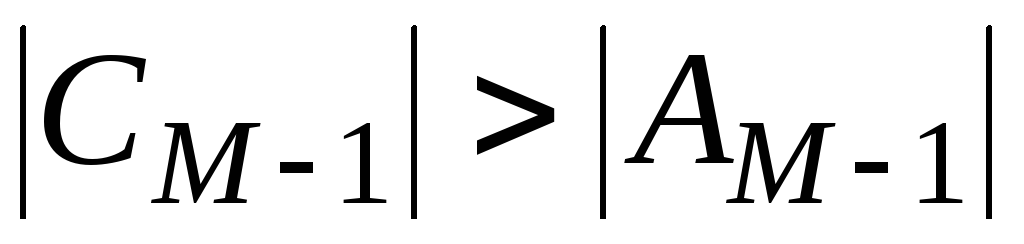 ,
,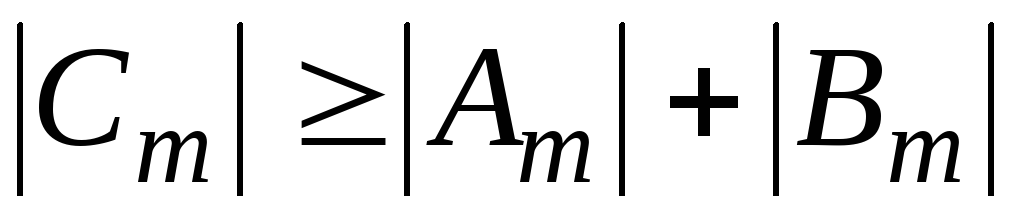 ,
, ,
,
то 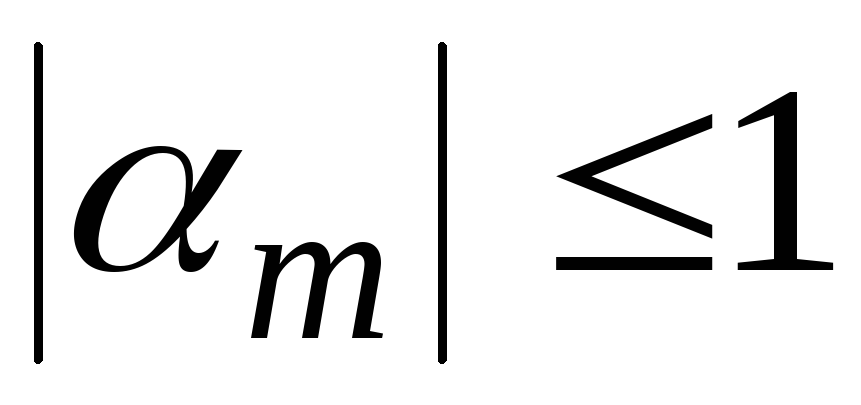 для
для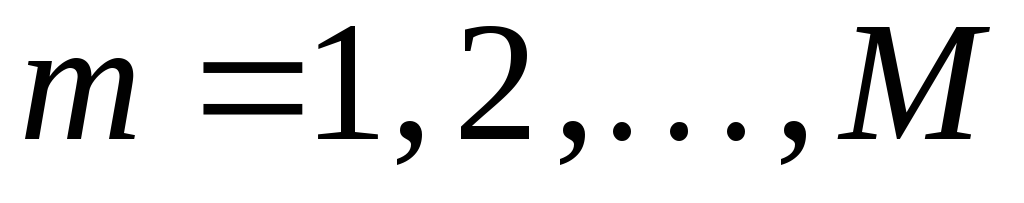 и метод прогонки можно применять.
и метод прогонки можно применять.
Доказательство. Неравенства длядокажем методом математической индукции.. Пусть при некоторомm выполняется неравенство , тогда
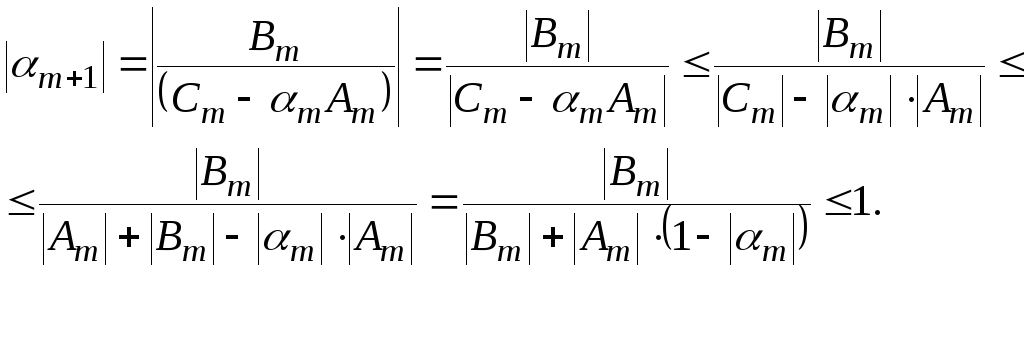
Неравенство доказано. Осталось доказать, что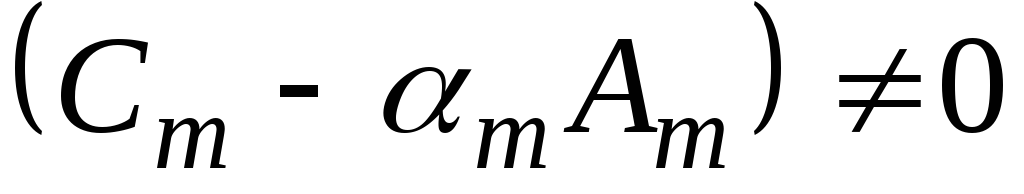 при
при . Зафиксируем любое из целых значений
. Зафиксируем любое из целых значений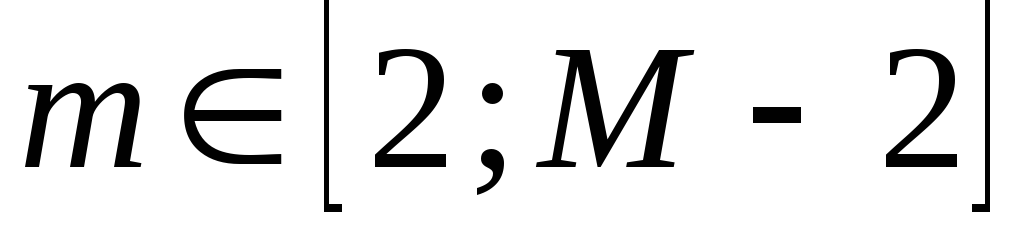 и рассмотрим разность:
и рассмотрим разность:
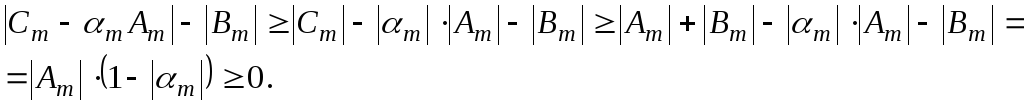
Отсюда 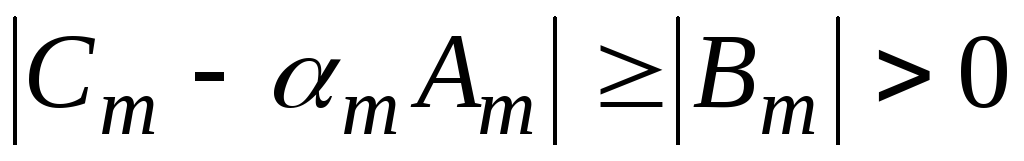 . И наконец, рассмотрим два оставшихся случая:
. И наконец, рассмотрим два оставшихся случая: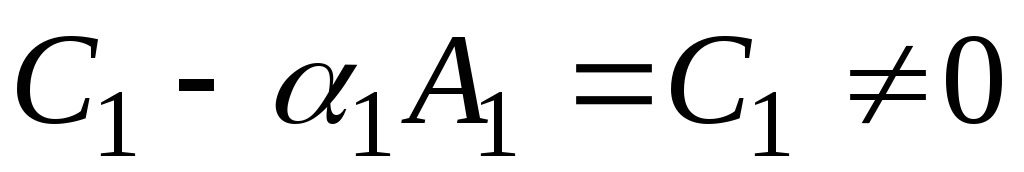 , так как
, так как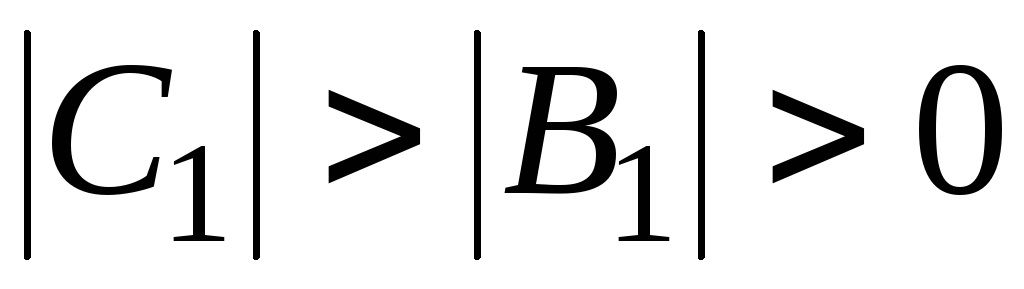 .
.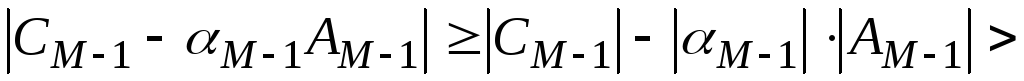
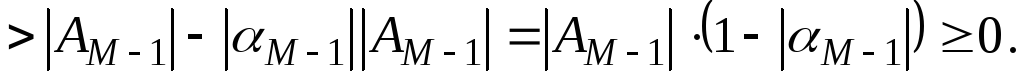 Теорема полностью доказана.
Теорема полностью доказана.
2. Численное интегрирование. Методы прямоугольников, трапеций.