1. Математическое моделирование и его погрешности. Погрешности метода решения и вычислительная погрешность.
Построение любой математической модели и ее реализация связаны с упрощением исходного объекта или явления и внесением погрешностей. Эти погрешности называются погрешностями модели. Погрешность модели является неустранимойпогрешностью. При переходе от математической модели к численному методу возникают погрешности, которые носят название погрешностей метода. Наиболее типичные погрешности метода - это погрешность дискретизациии погрешность усечения (обрыва).При реализации численного метода на ЭВМ возникают погрешности округления.
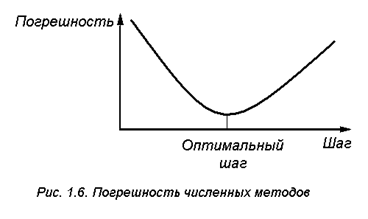
становимся подробней на погрешностях метода и вычислительных погрешностях. В диапазоне пространственно-временных промежутков, в которых функционируют электротехнические устройства, пространство и время можно считать непрерывными субстанциями. Аналитические зависимости электрических величин как функции пространства (линии, площади или объема) и времени обладают этой непрерывностью за исключением точек скачков и разрывов. При этом для любой точки пространства или любого момента времени (в рамках задачи) известно значение данной величины - тока, напряжения, индукции и т. д. Численные же методы дают возможность найти зависимости между величинами дискретно,т.е. в отдельных точках, и непосредственные результаты расчетов могут быть представлены только в табличном виде. Шаг по аргументу, например, времени t, с которым заполняется таблица, называется шагом дискретизации h. Точки аргумента, в которых известны значения функций, называются узлами.Характер же изменения функции между узлами и ее промежуточные значения неизвестны. Чем больше шаг дискретизации, тем выше погрешность численного решения. Точность же решения уравнения при наличии аналитической зависимости от шага не зависит. В основном погрешность дискретизации связана с тем, что для построения численных методов используются приемы, связанные с заменой производных функций конечными разностями [10]. При стремлении шага h к нулю погрешность дискретизации тоже стремится к нулю. Второй погрешностью метода является погрешность усечения (обрыва). Эта погрешность связана с тем, что многие функции, входящие в математическое описание модели, представляются в виде усеченных бесконечных степенных рядов аргумента. Это и дает ошибку усечения (обрыва). Например, sin(x) можно представить в виде степенного ряда
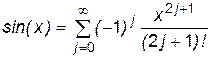. (1.6)
При сохранении двух членов ряда будем иметь усеченную формулу для вычисления синуса:
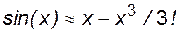
2. Метод наименьших квадратов: точечный и интегральный.
S (ао, а1, ... , ат)= L [Yi - f (xi)] 2, m « п.
