Первообразная и неопределенный интеграл

Функция 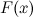называется первообразной для функции 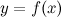на промежутке 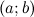, конечном или бесконечном, если функция 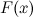дифференцируема в каждой точке этого промежутка и ее производная удовлетворяет следующему равенству:

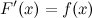
Последнее равенство можно записать через дифференциалы:

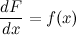или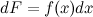

Первообразная 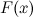имеет конечную производную, а, следовательно, является непрерывной функцией.

Теорема

(О бесконечном множестве первообразных для функции)

Если функция 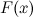является первообразной для функции 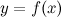на некотором промежутке, то и функция 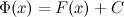, где 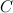- произвольная постоянная, также будет первообразной для функции 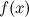на рассматриваемом промежутке.

Таким образом, если функция 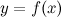имеет первообразную, то она имеет бесконечное множество первообразных.

Теорема

(Об общем виде первообразной для функции)

Если функци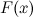и и 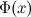- две любые первообразные функции 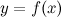, то их разность равна некоторой постоянной, то есть

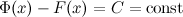
Последнюю теорему можно сформулировать иначе: каждая функция, которая является первообразной для функции 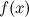, может быть представлена в виде .

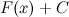Неопределенный интеграл

Определение

Совокупность всех первообразных функции 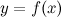, определенных на заданном промежутке, называется неопределенным интегралом от функции 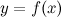и обозначается символом 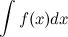. То есть

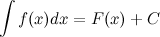
Знак 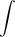называется интегралом, 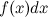- подынтегральным выражением, 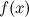- подынтегральной функцией, а - переменной интегрирования.

Операция нахождения первообразной или неопределенного интеграла от функции 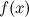называется интегрированием функции 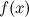. Интегрирование представляет собой операцию, обратную дифференцированию.

Геометрическая интерпретация неопределенного интеграла

Неопределенный интеграл представляет собой семейство параллельно расположенных кривых 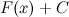, где каждому конкретному числовому значению постоянной 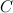соответствует определенная кривая из указанного семейства.

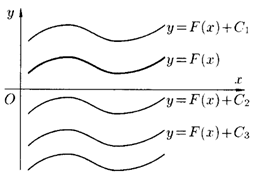
График каждой кривой из семейства называется интегральной кривой.

Теорема

Каждая непрерывная на промежутке 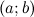функция, имеет на этом интервале первообразную.