Дифференциал функции
Пусть функция 
дифференцируема в точке 
, то есть приращение этой функции можно представить в виде суммы двух слагаемых: линейного относительно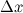 
и нелинейного членов:
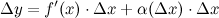
где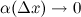 
при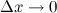 
.
Определение
Дифференциалом функции называется линейная относительно 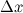часть приращения функции. Она обозначается как 
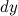или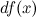 
. Таким образом:
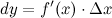
Геометрический смысл дифференциала
Дифференциал функции в точке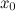 
равен приращению ординаты касательной, проведенной к графику функции в этой точке, соответствующему приращению аргумента .
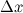