Определение
Если и существует
, то формула Тейлора принимает вид:
.
Формулу (1) называют формулой Маклорена.
Разложение в ряд Маклорена элементарных функций
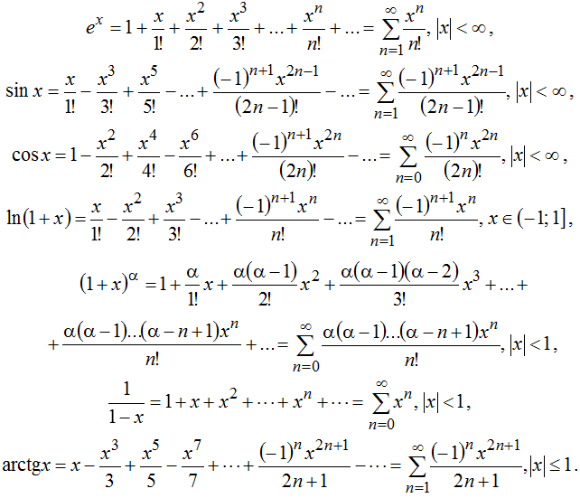
Замечание 1. Пусть функция бесконечно дифференцируема на интервале
Если эта функция является четной, то её производная – нечетная функция, и, наоборот, производная нечетной функции – четная функция.
Пусть
– четная функция, тогда:
,
.
Дифференцируя это тождество, получаем.
Это означает, что – нечетная функция. Аналогично рассматривается случай, когда
– нечетная функция.
Отсюда следует, что для нечетной функции выполняютcя условия
,
, а для четной функции
– условия
,
, так как любая непрерывная нечетная функция принимает при
значение нуль.
Поэтому формулу (1) для бесконечно дифференцируемой четной функции можно записать в виде:
,
а для нечетной функции – в виде:
.

