Первый достаточный признак. Пусть функция 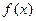 непрерывна в некотором интервале, содержащем критическую точку
непрерывна в некотором интервале, содержащем критическую точку 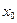 и дифференцируема во всех точках этого интервала (кроме, быть может самой точки
и дифференцируема во всех точках этого интервала (кроме, быть может самой точки 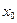 ). Тогда, если:
). Тогда, если:
а) 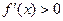 при
при 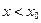 ,
, 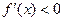 при
при 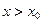 , то в точке
, то в точке 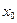 функция
функция 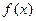 достигает максимума;
достигает максимума;
б) 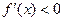 при
при 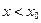 ,
, 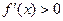 при
при 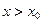 , то в точке
, то в точке 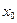 функция
функция 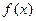 достигает минимума.
достигает минимума.
 Второй достаточный признак экстремума. Пусть функция
Второй достаточный признак экстремума. Пусть функция 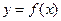 имеет в точке
имеет в точке 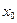 производную
производную 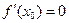 и непрерывную вторую производную
и непрерывную вторую производную 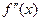 . Тогда, если
. Тогда, если 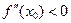 в точке
в точке 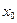 будет максимум, а если
будет максимум, а если 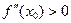 в точке
в точке 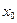 будет минимум.
будет минимум.
Теорема (первое достаточное условие экстремума в терминах первой производной)
Пусть функция определена и дифференцируема в некоторой окрестности точки
, кроме, быть может, самой точки
и непрерывна в этой точке. Тогда:
- Если производная
меняет знак с “-” на “+” при переходе через точку
:
и
, то
– точка строго минимума функции
- Если производная
меняет знак с “+” на “-” при переходе через точку
:
и
, то
– точка строго максимума функции
Доказательство
Пусть, например, меняет знак с “-” на “+”. Рассмотрим точку
на сегменте
Воспользуемся теоремой о конечных приращениях Лагранжа:
,
. Поскольку при переходе через точку
функция меняет знак с “-” на “+”, то
и
, то
Аналогично рассмотрим сегмент , получим
– точка строгого минимума функции.
Замечания:
Если – точка строго экстремума, то из этого не следует, что производная
меняет знак при переходе через точку
Теорема (второе достаточное условие строгого экстремума в терминах второй производной)
Пусть дана функция , она определена в некоторой окрестности точки
, ее первая производная
и пусть
, тогда:
- Если
, то точка
– точка строгого минимума;
- Если
, то точка
– точка строгого максимума.
Доказательство
Докажем теорему для первого случая, когда . По скольку
непрерывна, то на достаточно малом интервале
, т.к
, то
возрастает в этом интервале.
, значит
на интервале
и
на интервале
.
Таким образом функция убывает на интервале
и возрастает на интервале
по первому достаточному условию экстремума функция в точке
имеет минимум.
Аналогично доказывается второй случай теоремы.
Замечания:
Если и
, то функция
может и не иметь экстремум в точке
Теорема (третье достаточное условие строгого экстремума в терминах производных порядка больше двух)
Пусть функция определена в некоторой окрестности точки
, и в этой точке существуют производные до n-го порядка пусть
,
и
,
Тогда:
- Если
(т.е
– четное), то
– точка экстремума:
- если
, то
– точка локального максимума;
- если
, то
– точка локального минимума;
- если
- Если
(т.е
– нечетное), то
– не является точкой экстремума.
Доказательство
Воспользуемся формулой Тейлора в окрестности точки с остатком в форме Пеано:
.
По скольку все производные до порядка включительно равны нулю получим:
Запишем полученное выражение в виде:
. Выражение
. Пусть
,
. Отсюда следует, что сохранение или изменение знака приращения функции во время перехода через точку
зависит от четности
. Последний факт и доказывает теорему.

