Теорема Ролля. Пусть функция f(x) непрерывна на отрезке [а, b], дифференцируема на (а, b), f(а) = f(b). Тогда существует хотя бы одна точка x, а < x < b, такая, что f'(x) = 0.
Доказательство:
1) если f(x) = const на [a, b], то f'(х) = 0, œх Î (a, b);
2) если f(x) ¹const на [a, b], то непрерывная на [a, b] функция достигает наибольшего и наименьшего значений в некоторых точках отрезка
[a, b]. Следовательно, maxf(x)или minf(x) обязательно достигается во внутренней точке x отрезка [a, b], а по теореме Ферма имеем, что f'(x) = 0.
Теорема доказана.
Теорема Коши. Пусть функции f(х) и g(х) непрерывны на отрезке
[a, b] и дифференцируемы на интервале (a, b), причем g'(х) ¹ 0, œх Î (a, b). Тогда на (a, b) найдется точка x, такая, что
 . (1)
. (1)
Доказательство.
Рассмотрим вспомогательную функцию 
 Функция F(х) непрерывна на [a, b], дифференцируема на (a, b), причем F(а) = F(b) = 0. Следовательно, по теореме Ролля на (a, b) существует точка x, такая, что F'(x) = 0:
Функция F(х) непрерывна на [a, b], дифференцируема на (a, b), причем F(а) = F(b) = 0. Следовательно, по теореме Ролля на (a, b) существует точка x, такая, что F'(x) = 0:

Следовательно:
 .
.
Теорема доказана.
Теорема Лагранжа. Пусть функция f(х) непрерывна на [a, b], дифференцируема на интервале (a, b). Тогда на (a, b) найдется точка x, такая, что

 (2)
(2)
Доказательство.
Из формулы (1) при g(x) = xполучаем формулу (2).
Теорема доказана.
Теорема Ферма:
Пусть функция 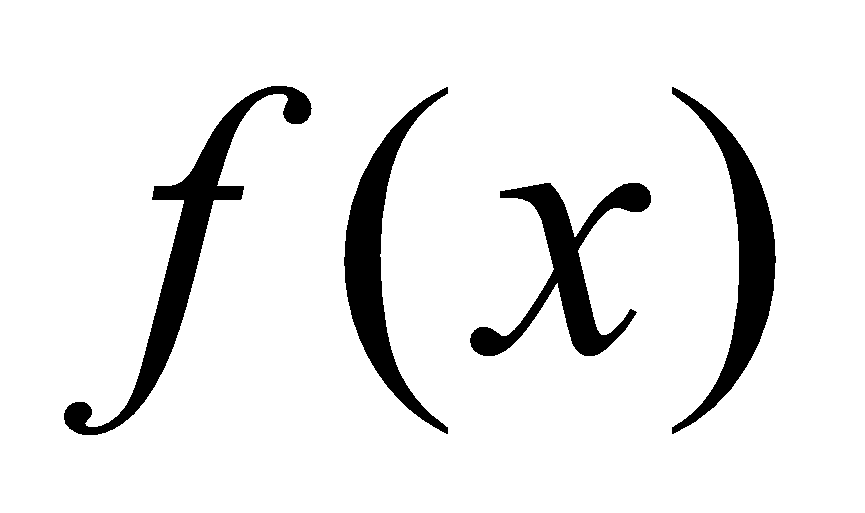 определена на
определена на 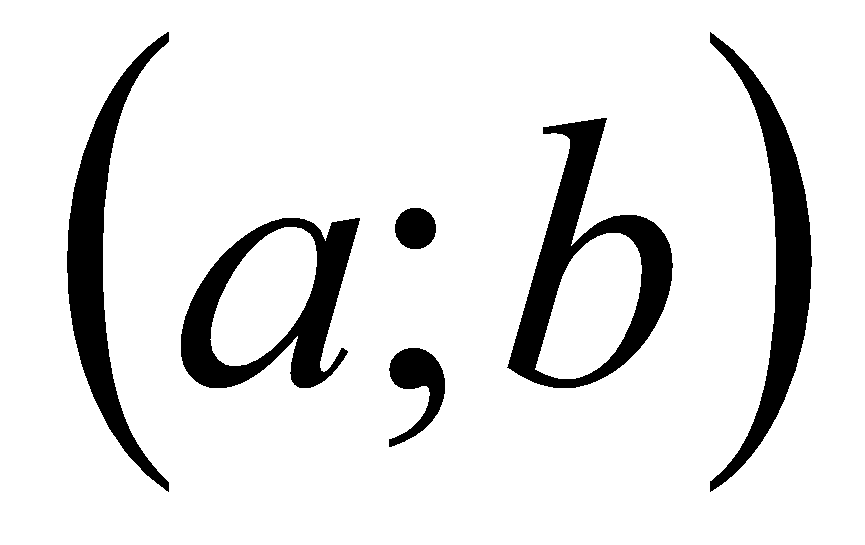 и достигает своего наибольшего и наименьшего значения (M и m) в некоторой
и достигает своего наибольшего и наименьшего значения (M и m) в некоторой 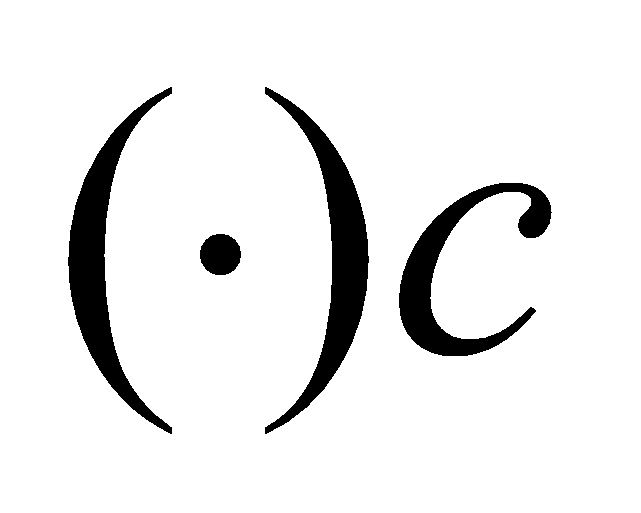 из
из 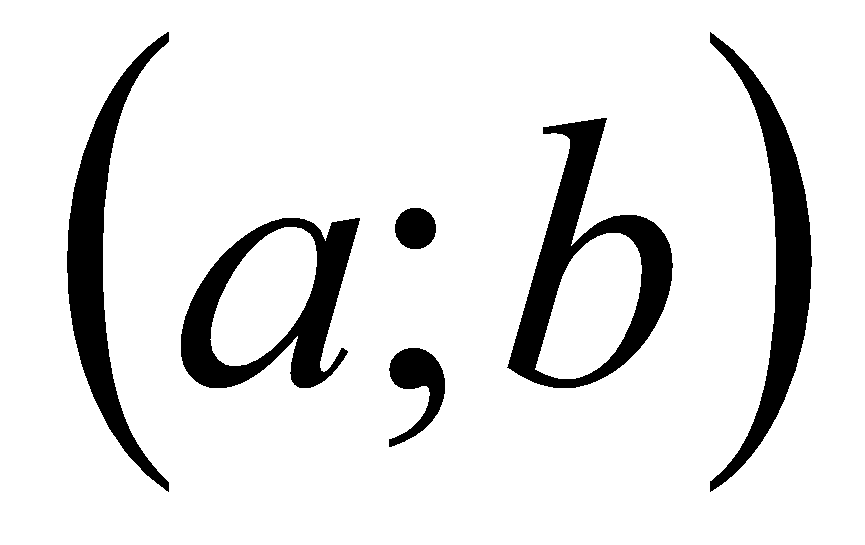 . Если существует производная
. Если существует производная 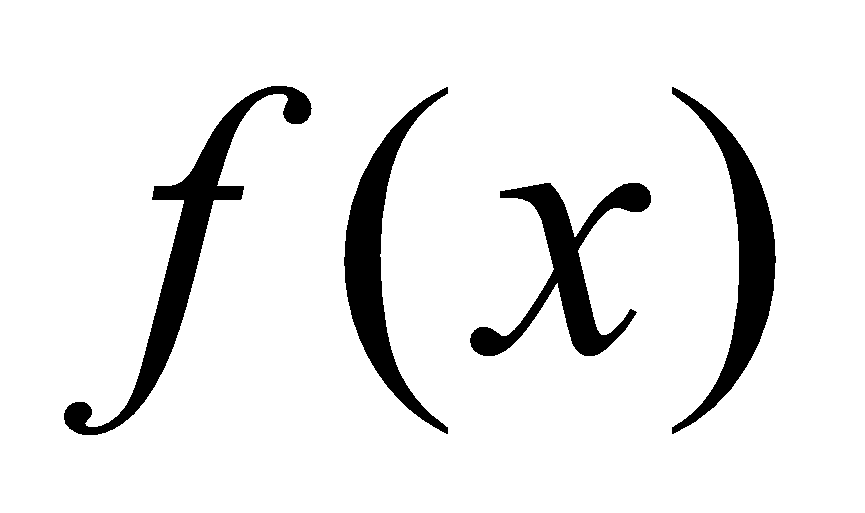 в
в 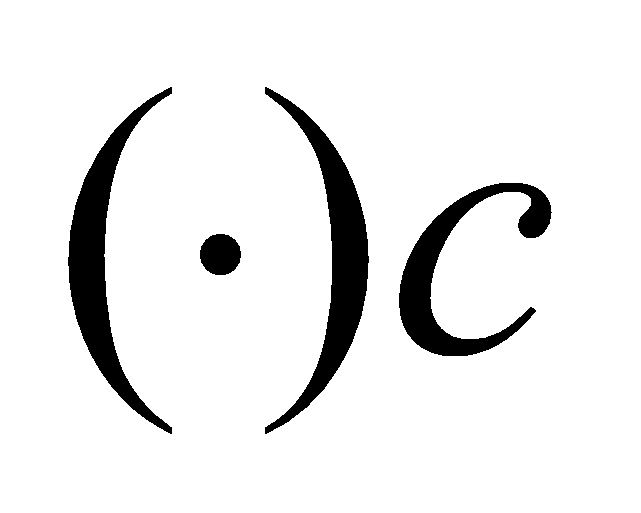 , то она обязательно равна 0.
, то она обязательно равна 0.
Доказательство:
Существует 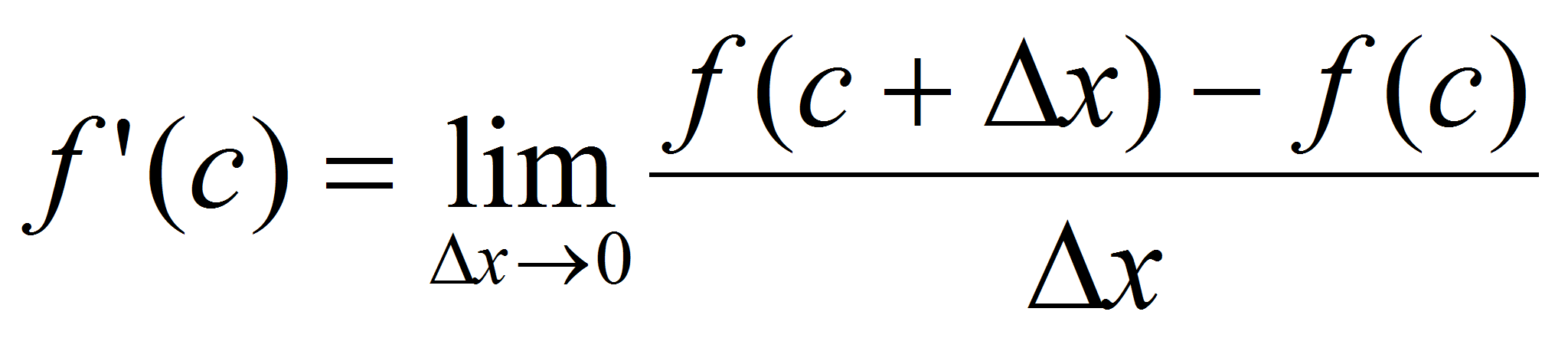 . Возможны два случая:
. Возможны два случая:
1)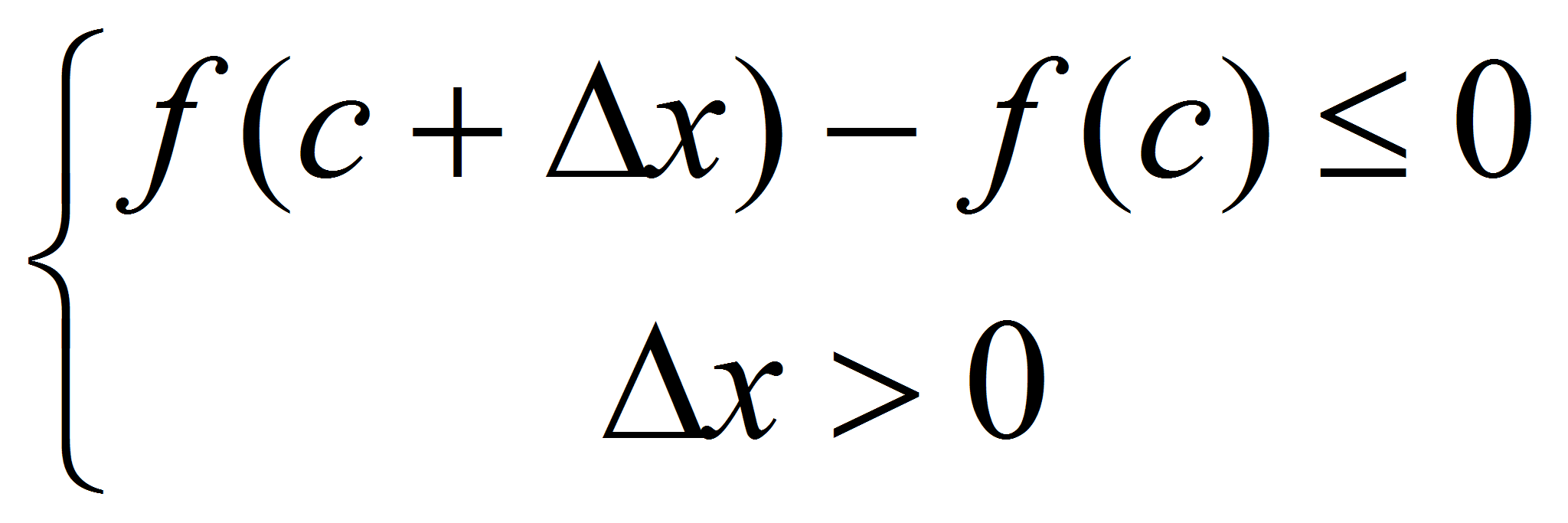 , =>
, => 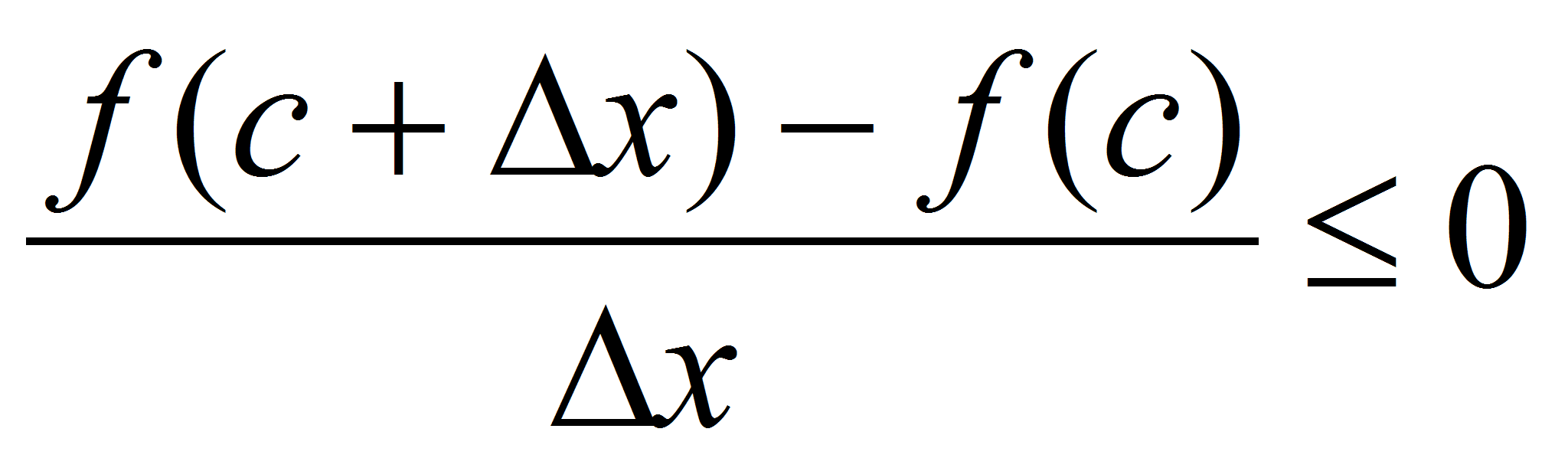 , =>
, =>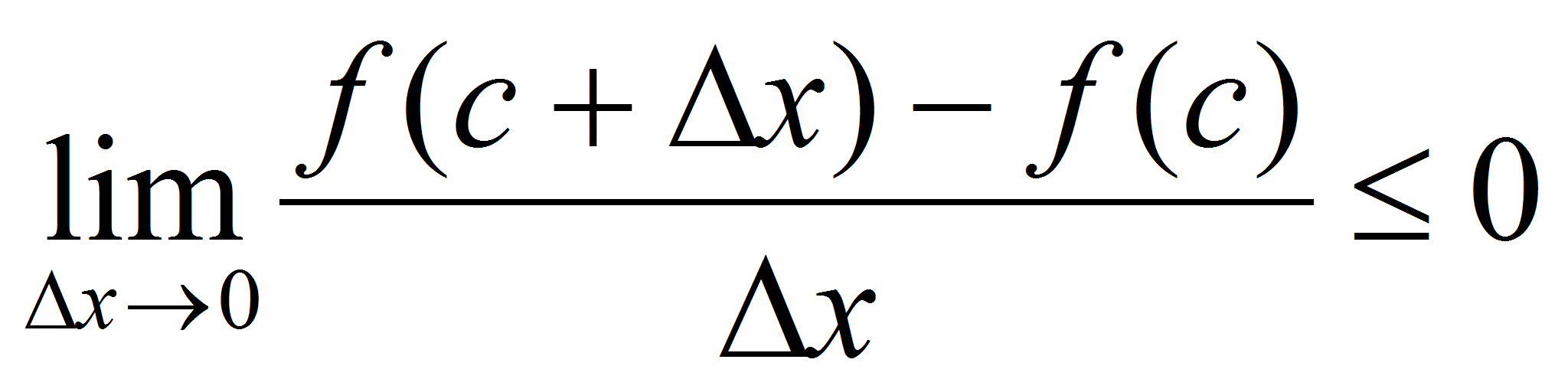 .
.
2)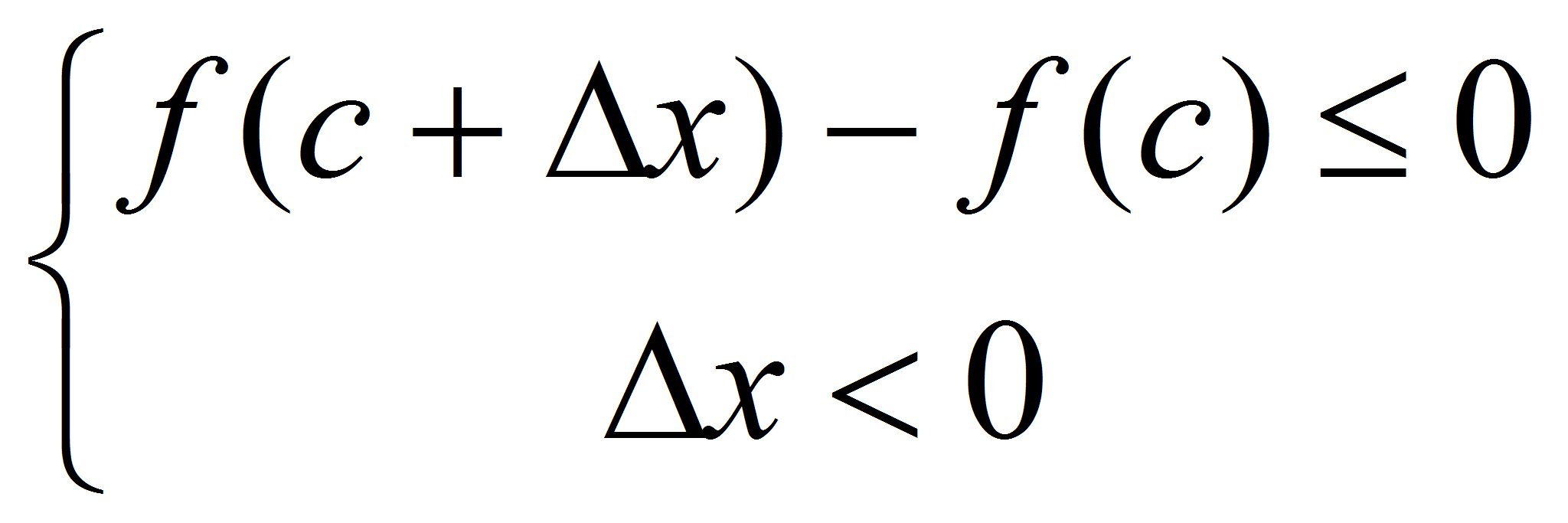 , =>
, => 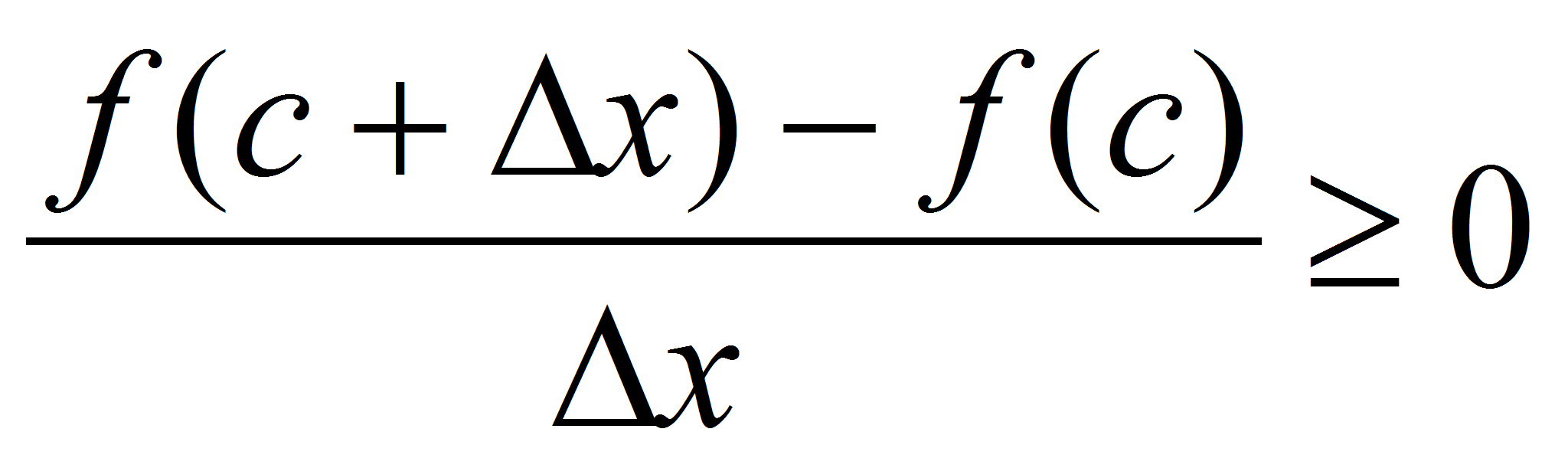 , =>
, =>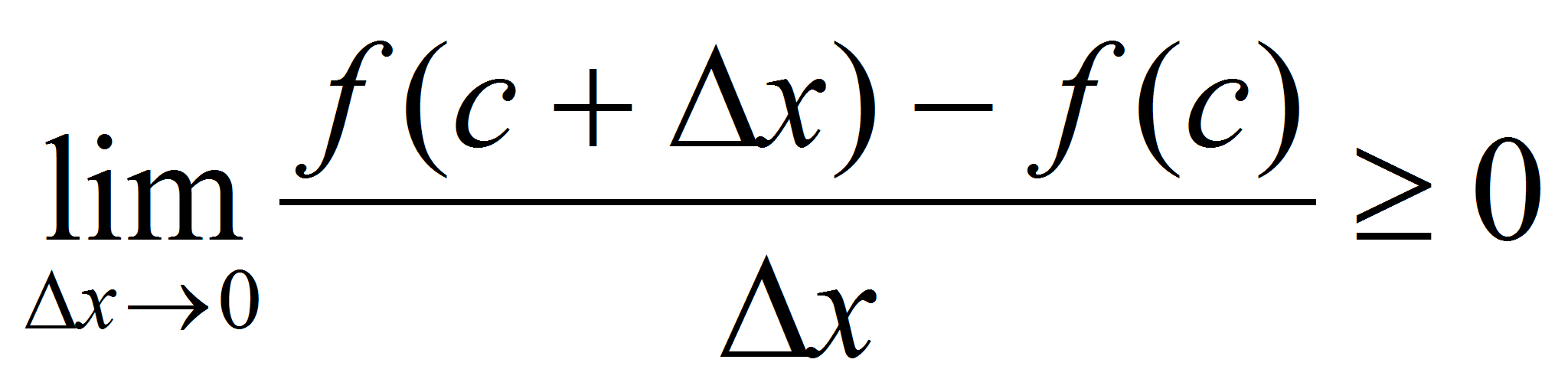 .
.
Из 1) и 2) следует, что 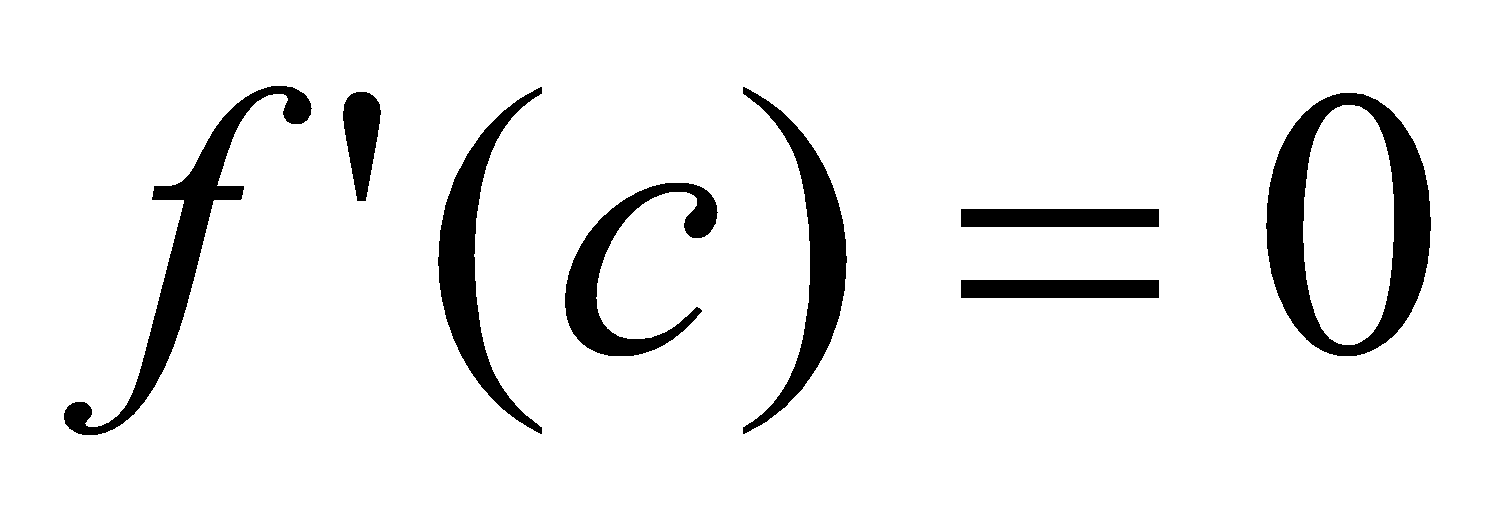
Теорема Ролля (о корнях производной):
Пусть функция 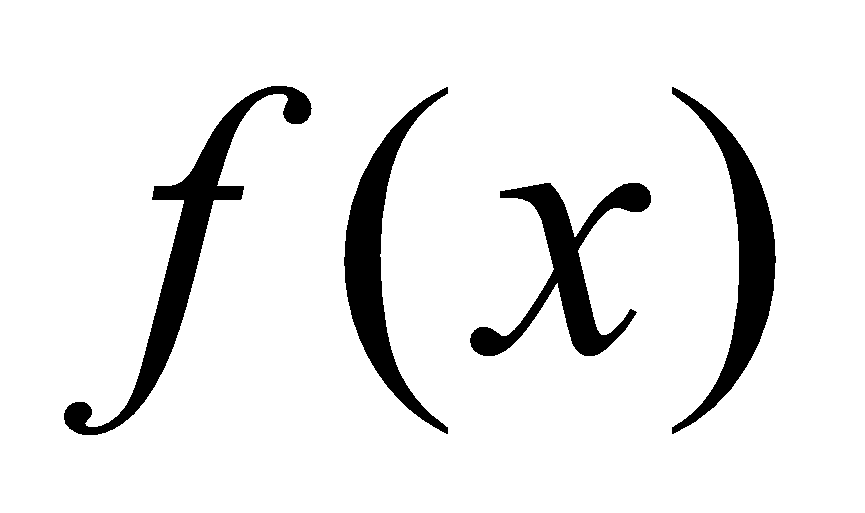 непрерывна на
непрерывна на 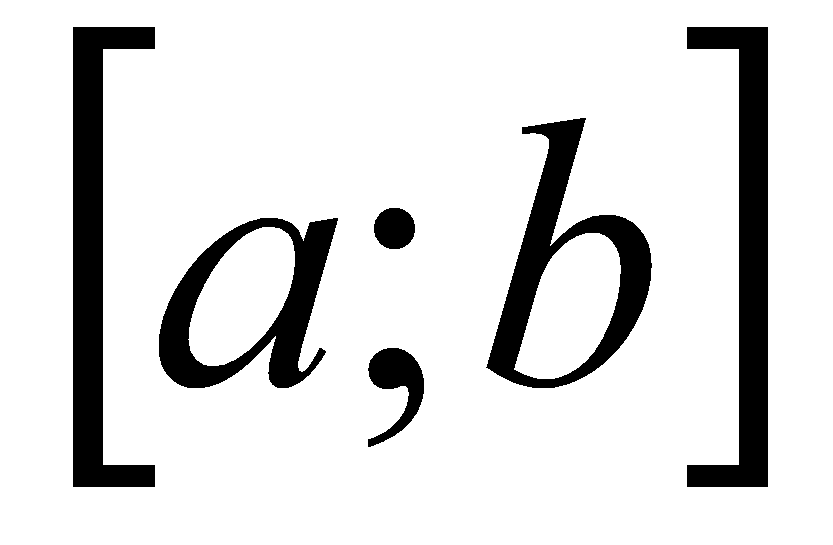 и дифференцируема на
и дифференцируема на 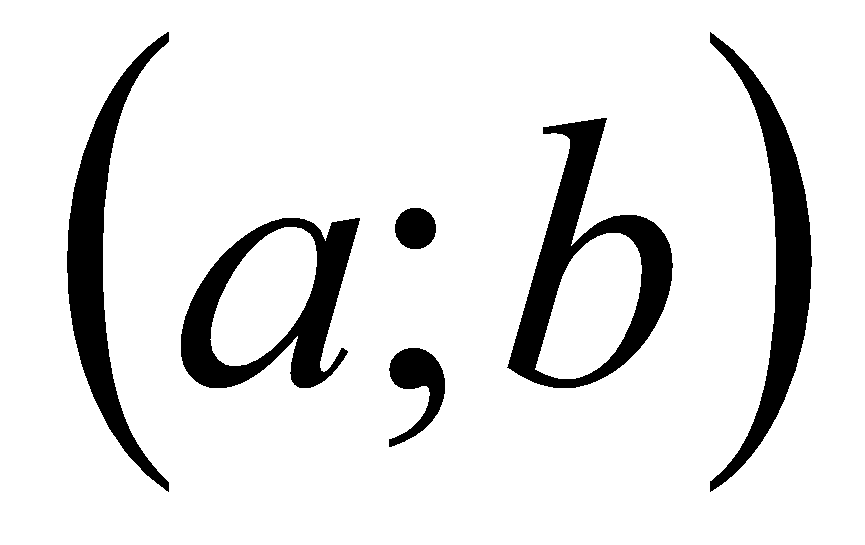 и на концах отрезка принимает одинаковые значения:
и на концах отрезка принимает одинаковые значения: 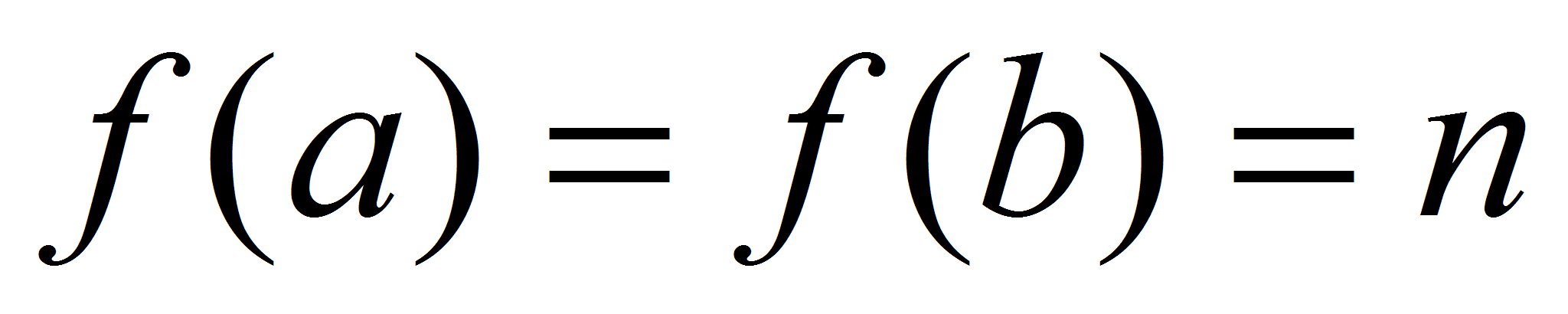 . Тогда существует хотя бы одна точка
. Тогда существует хотя бы одна точка 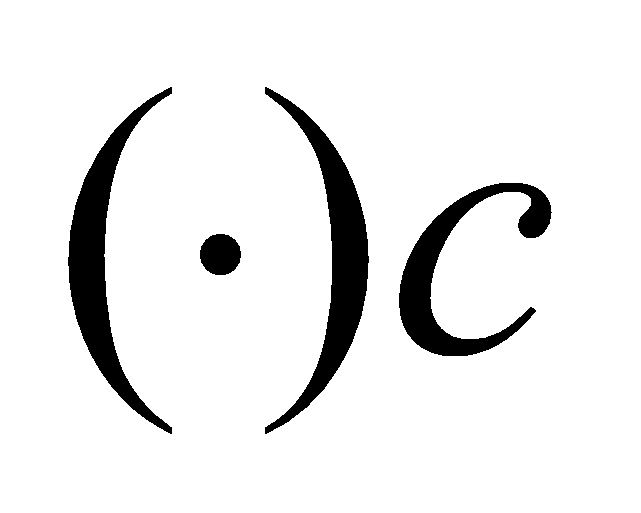 из
из 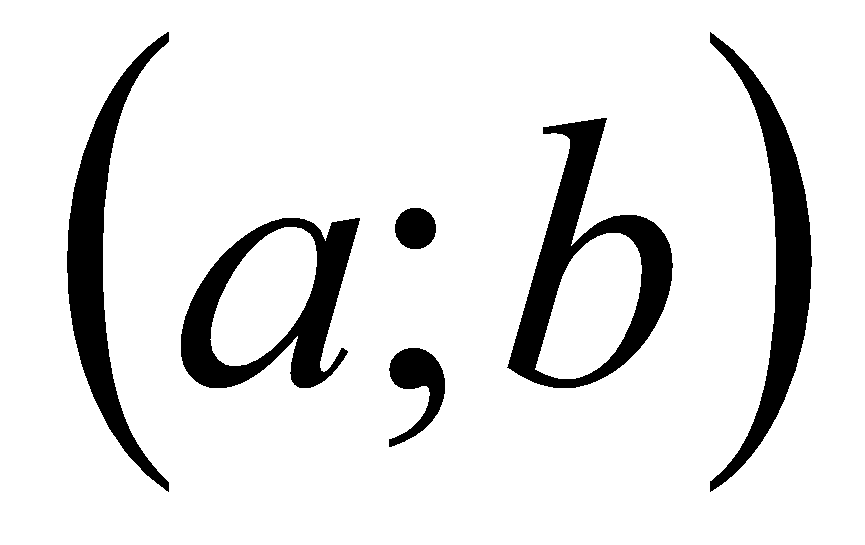 , производная в которой
, производная в которой 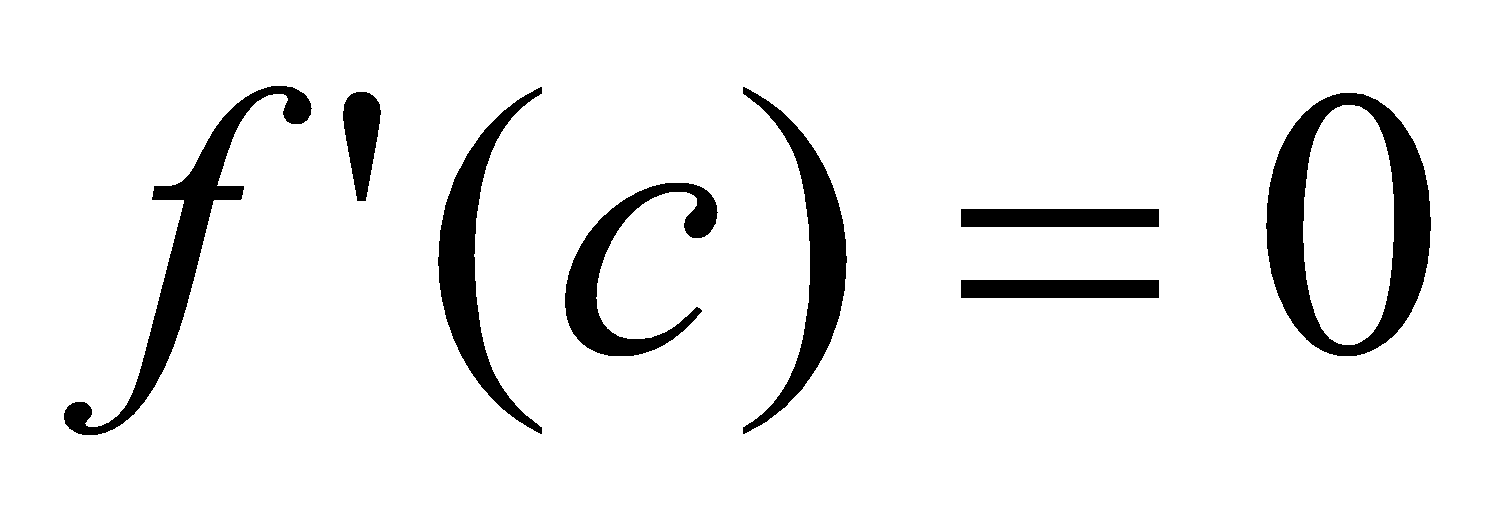 .
.
Доказательство:
Непрерывная 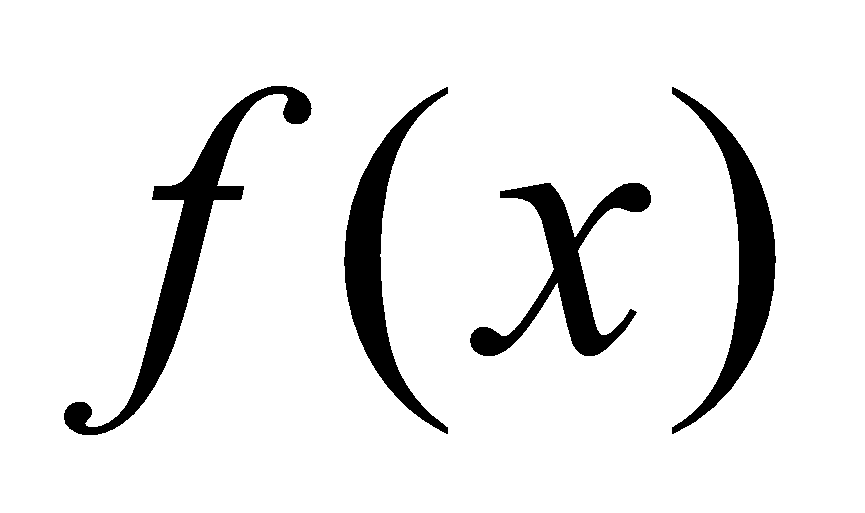 достигает на
достигает на 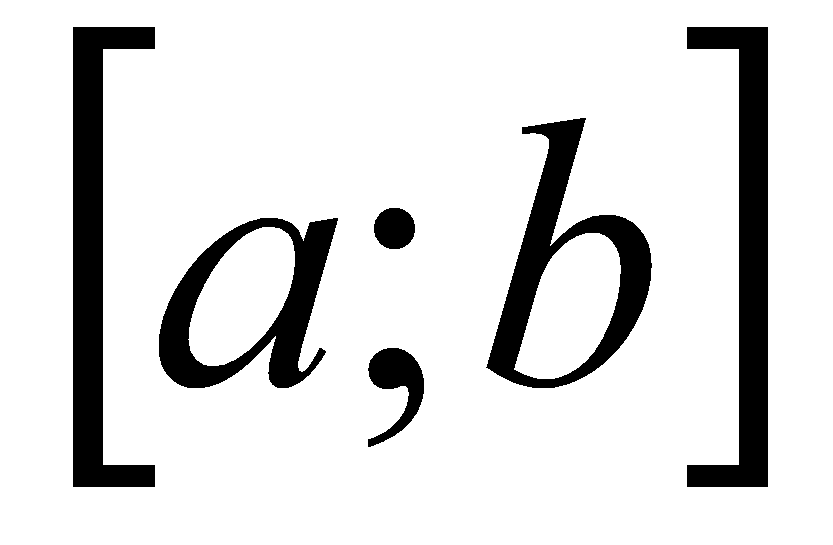 M и m. Тогда возможны два случая:
M и m. Тогда возможны два случая:
1)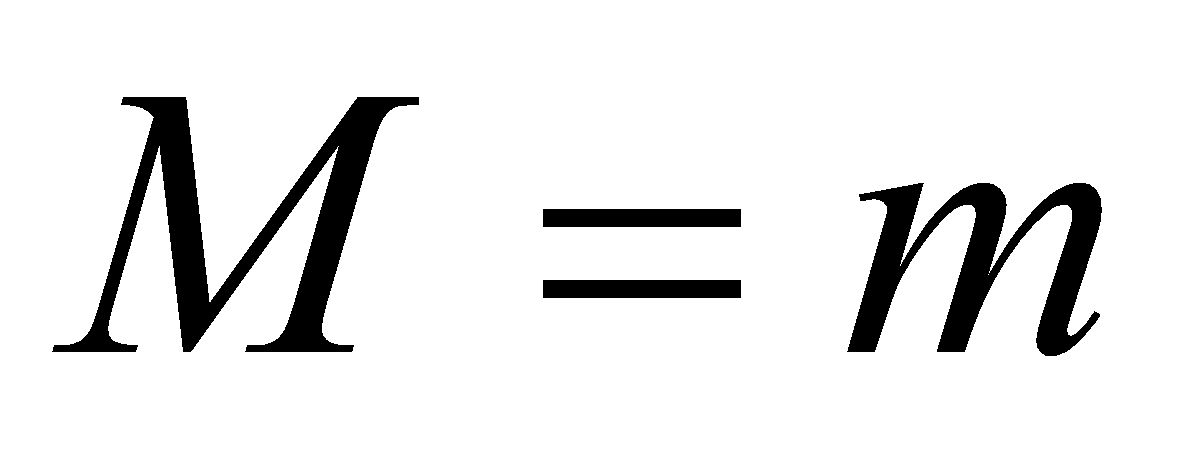 , =>
, =>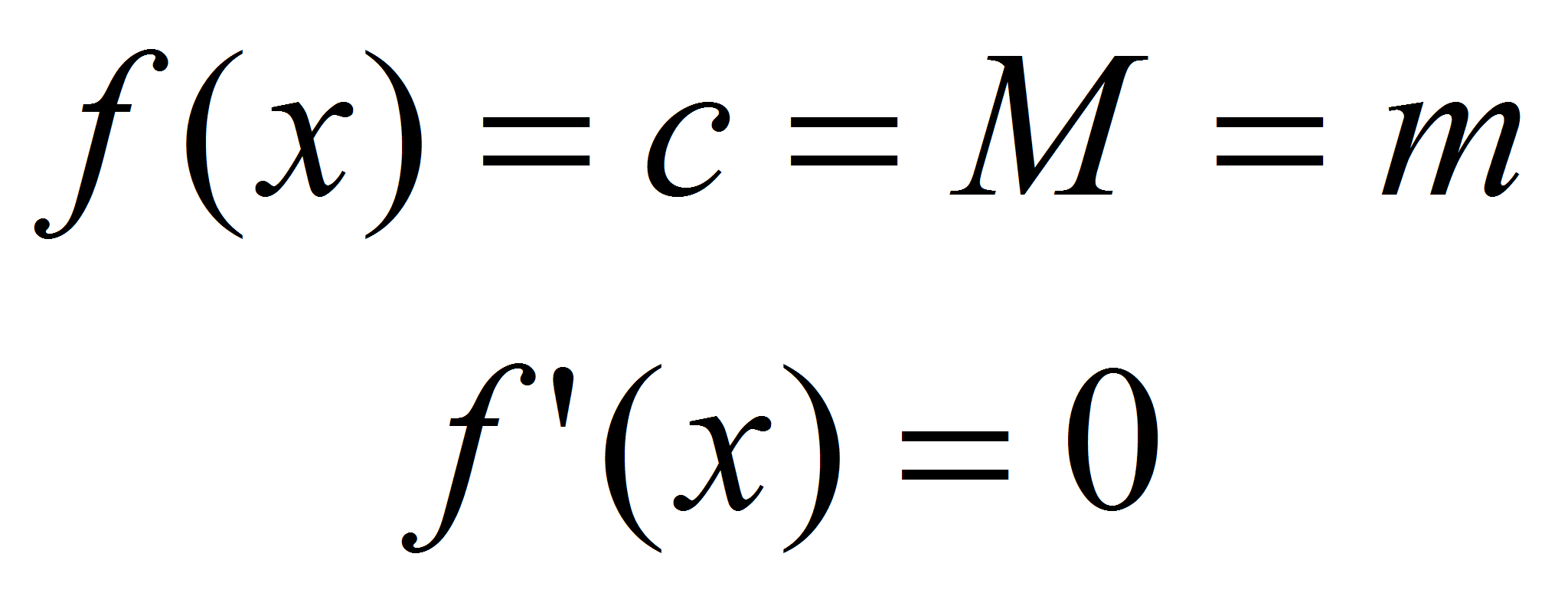
2) 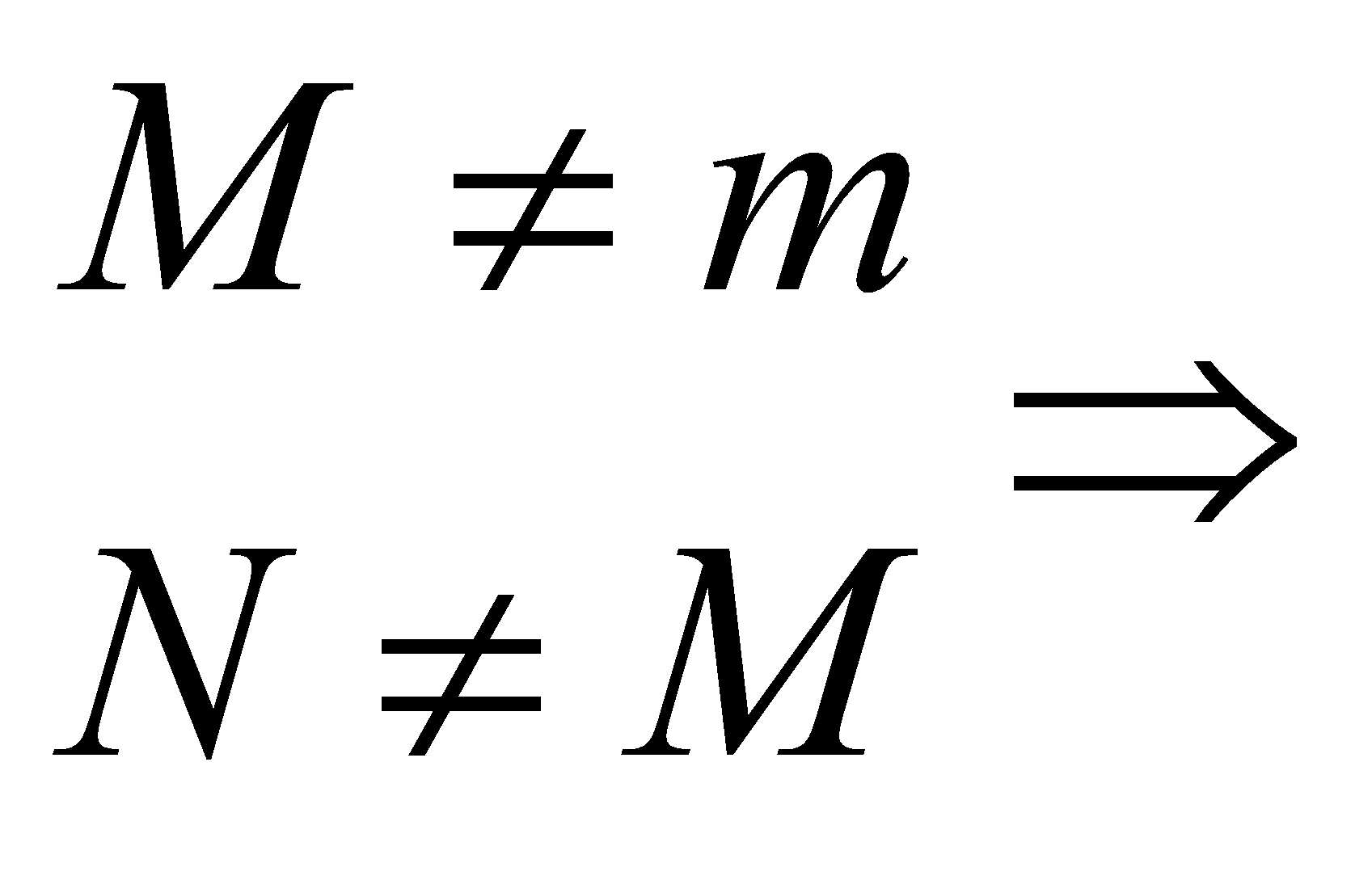 наибольшее значение достигается внутри интервала
наибольшее значение достигается внутри интервала 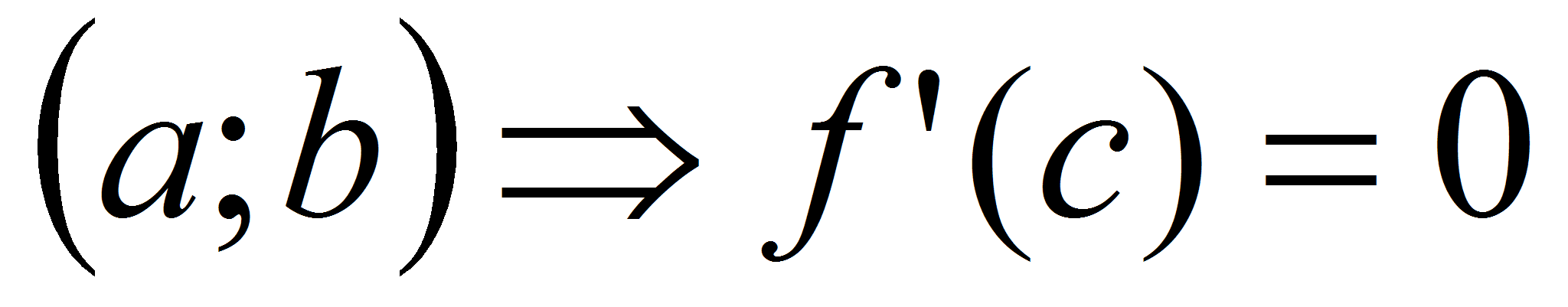 по теореме Ферма.
по теореме Ферма.
Теорема Лангража (о конечных приращениях):
Пусть функция 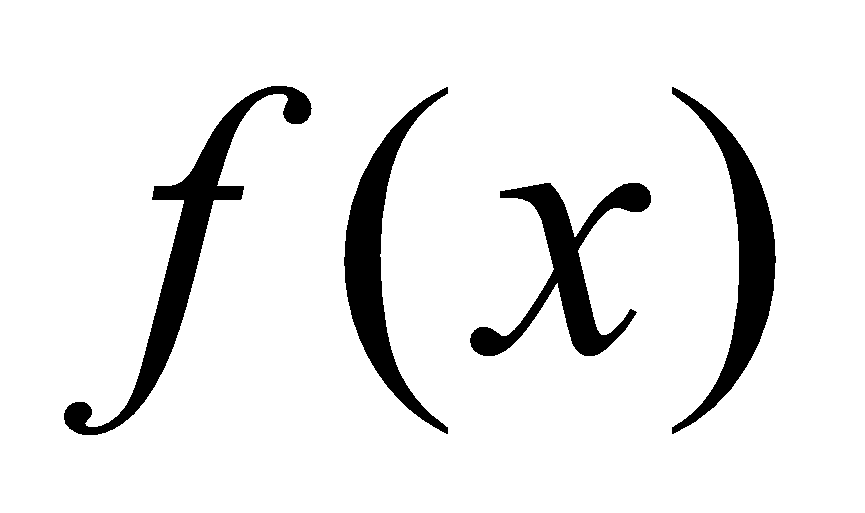 непрерывна на
непрерывна на 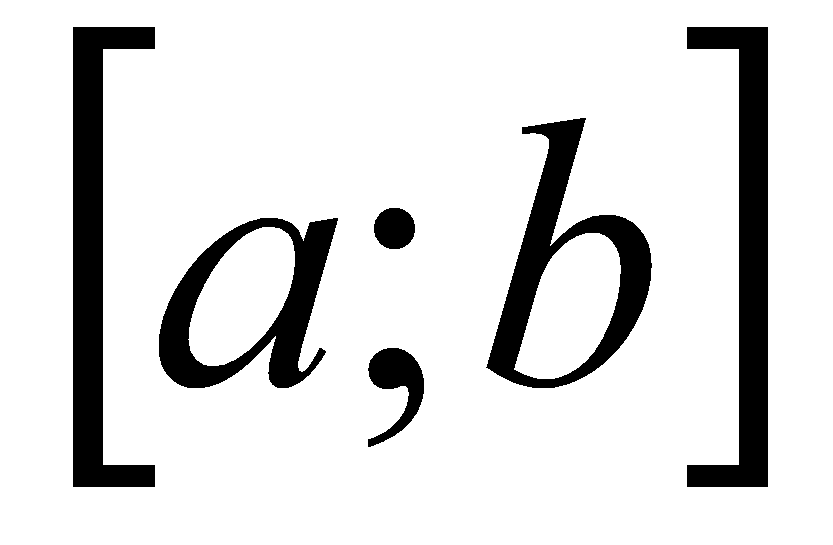 и дифференцируема на
и дифференцируема на 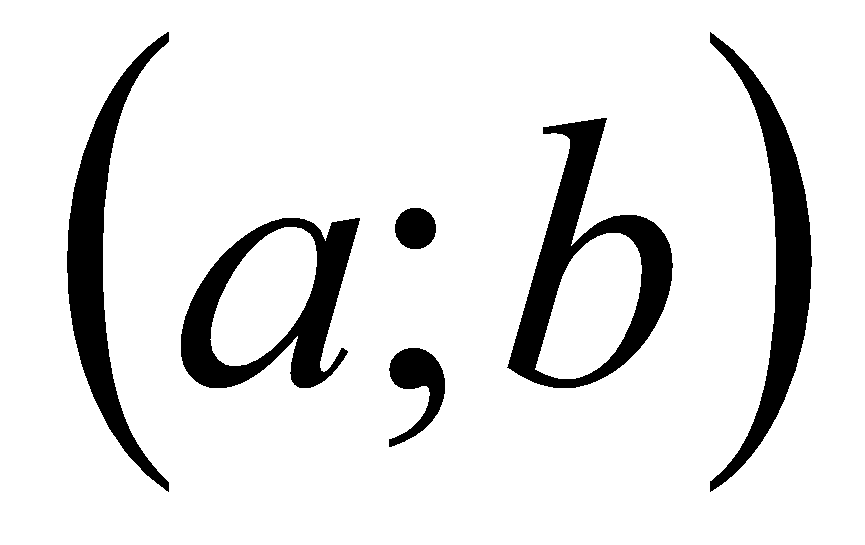 . Тогда существует хотя бы одна
. Тогда существует хотя бы одна 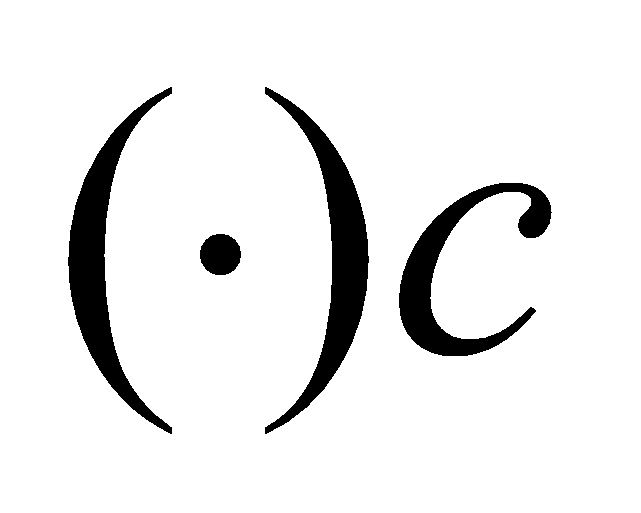 из
из 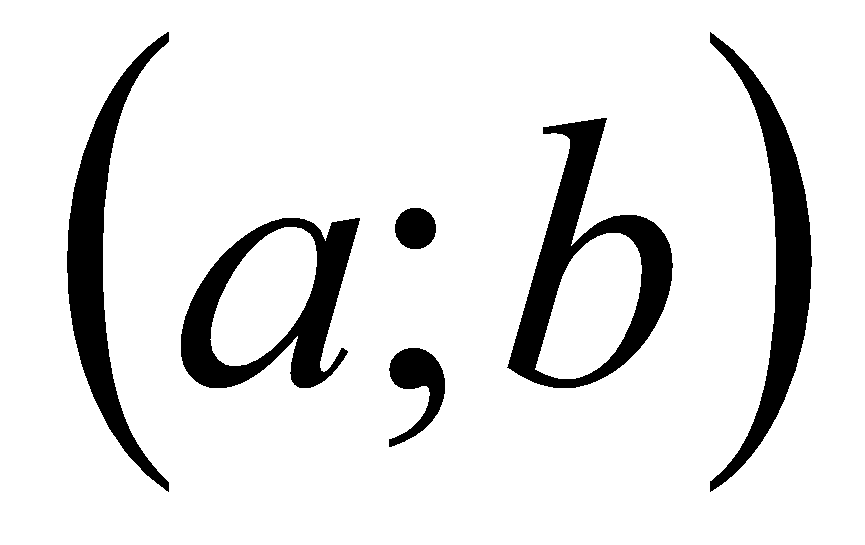 , для которой выполняется следующее равенство:
, для которой выполняется следующее равенство: 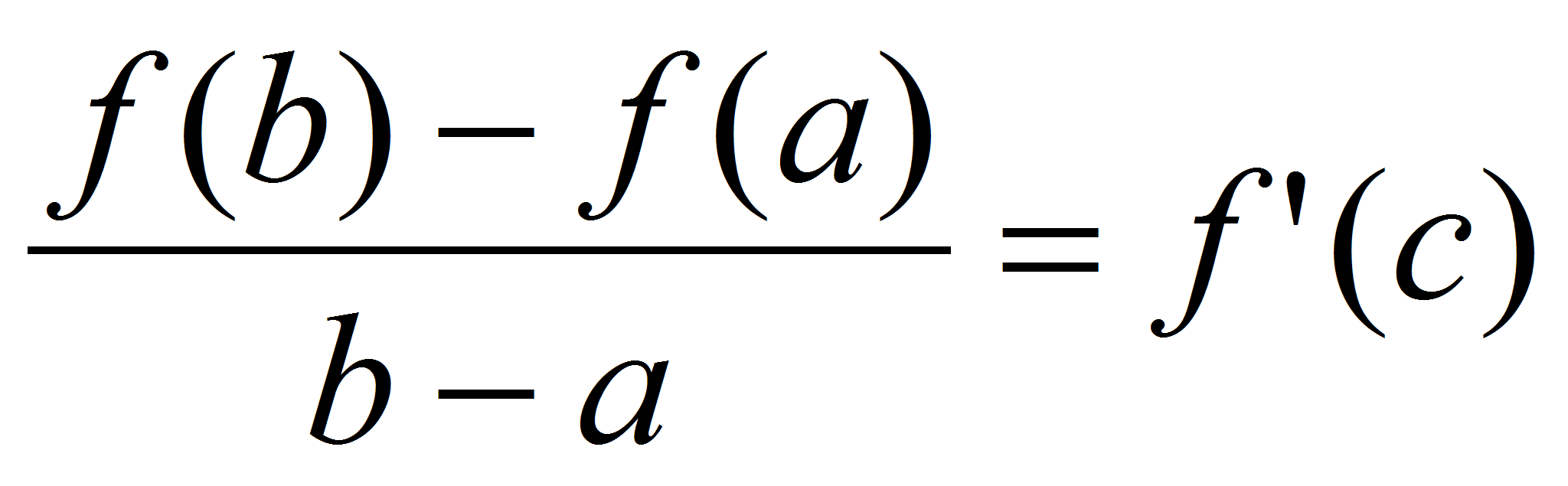 .
.
Доказательство:
Введем функцию 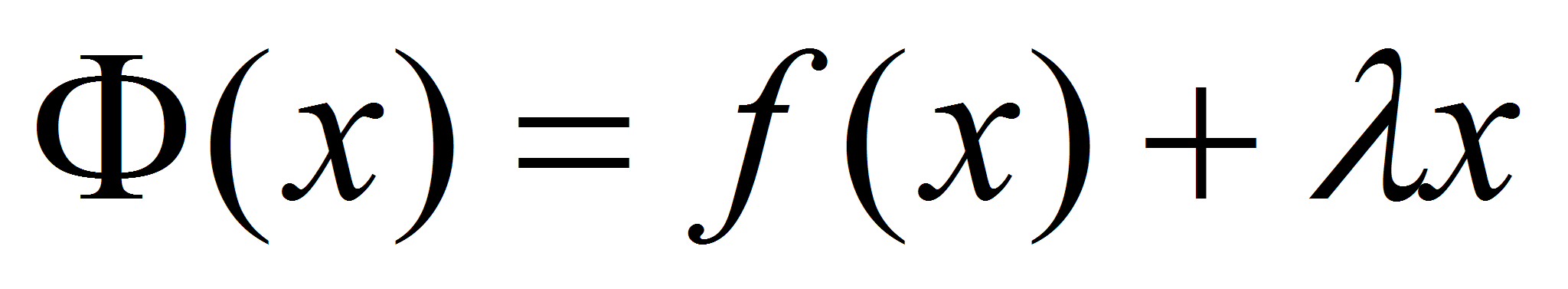 . (непрерывная на
. (непрерывная на 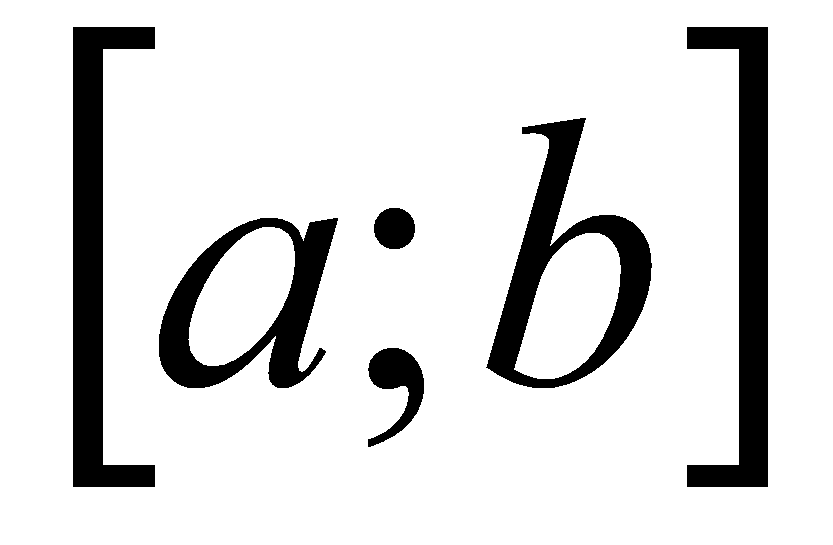 и дифференцируемая на
и дифференцируемая на 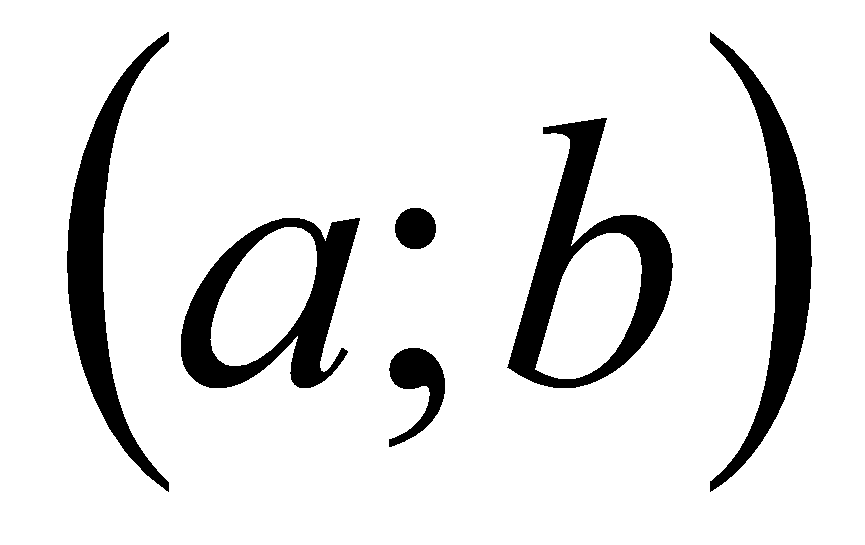 ).
).
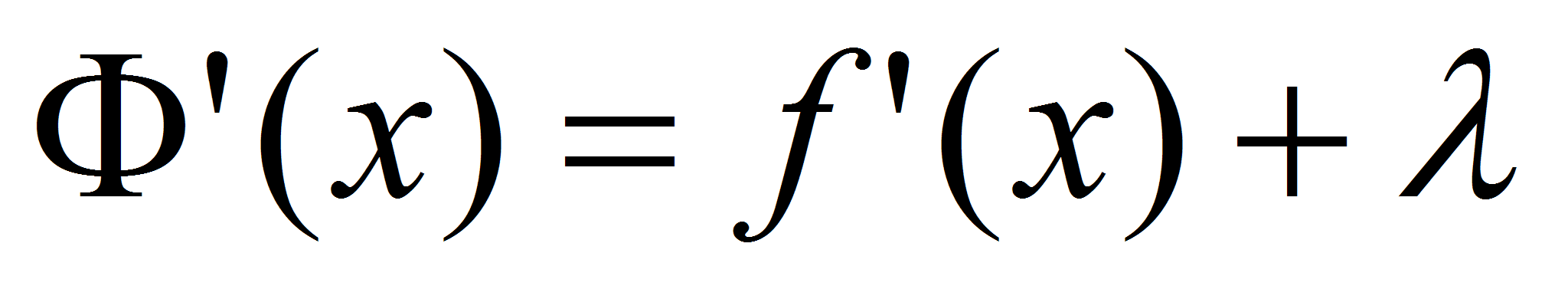
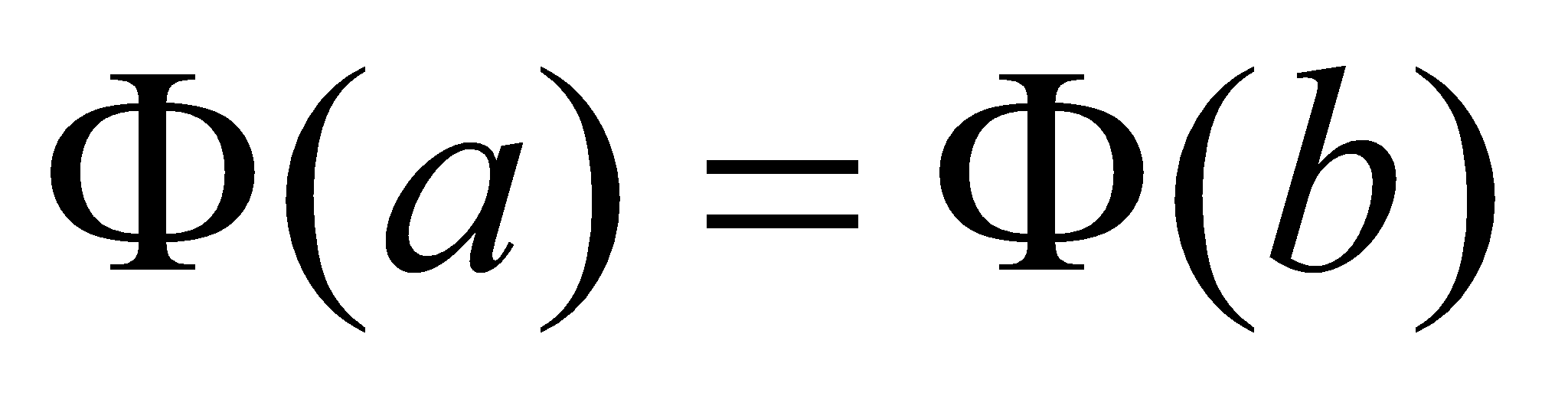
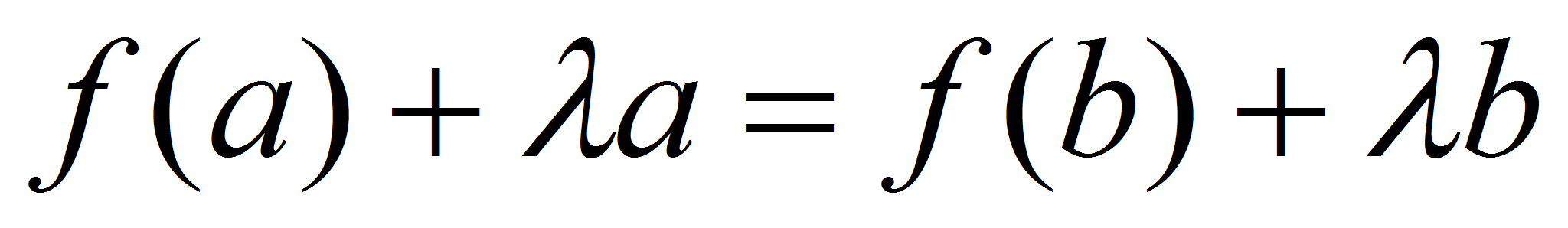
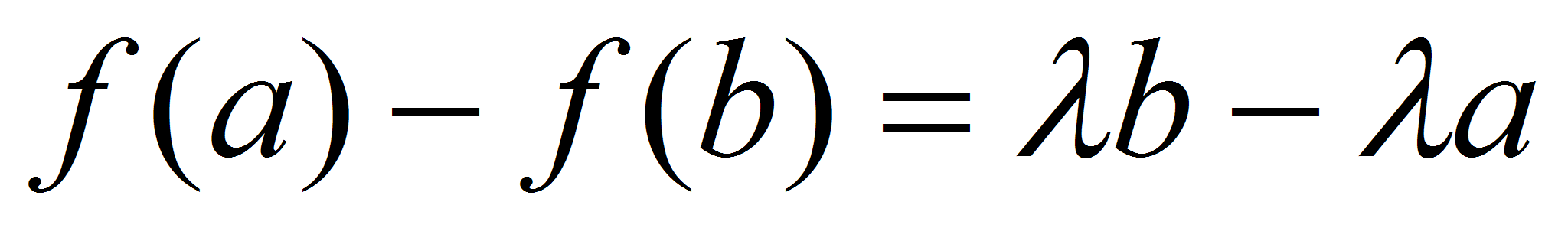
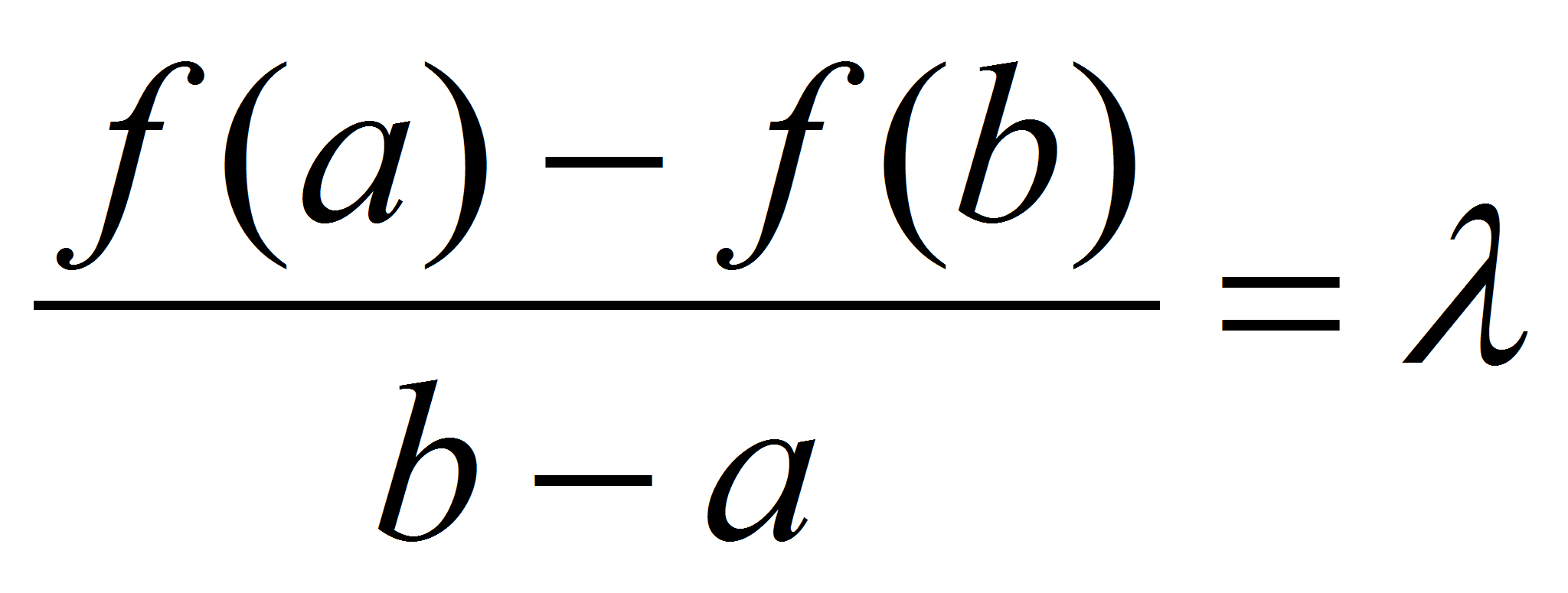 ,
,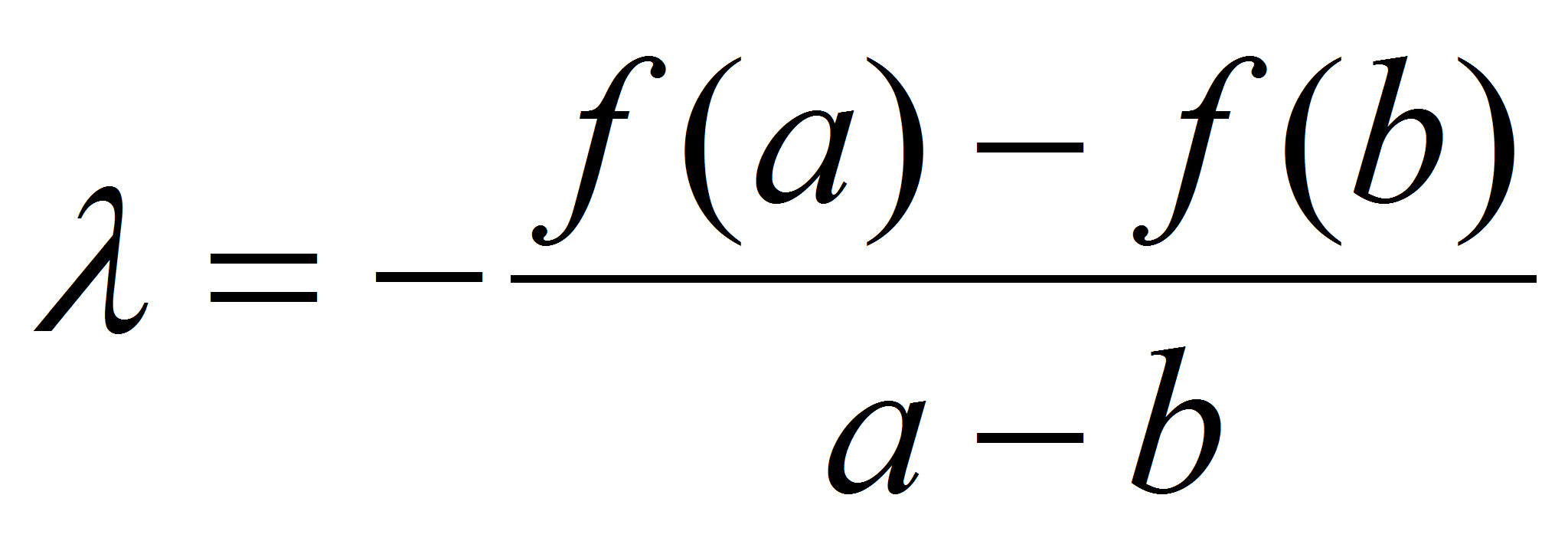
Функция 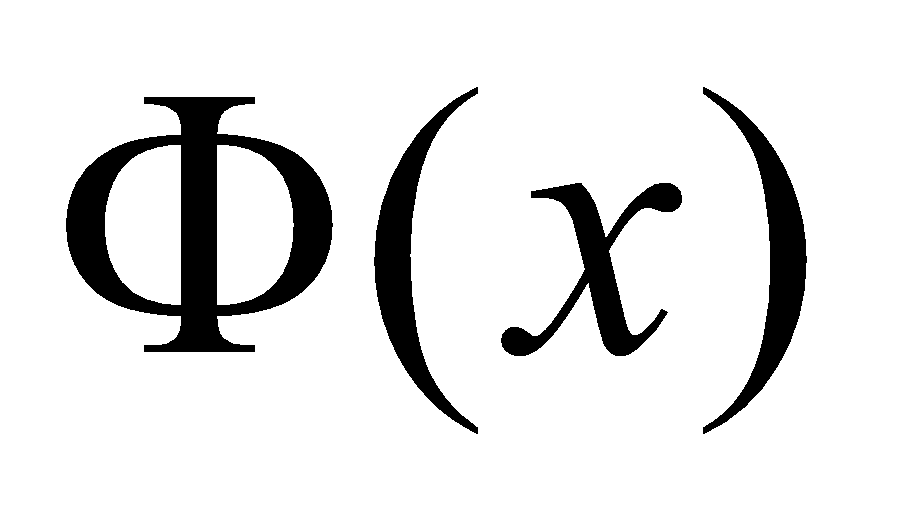 удовлетворяет Теореме Ролля
удовлетворяет Теореме Ролля  существует
существует 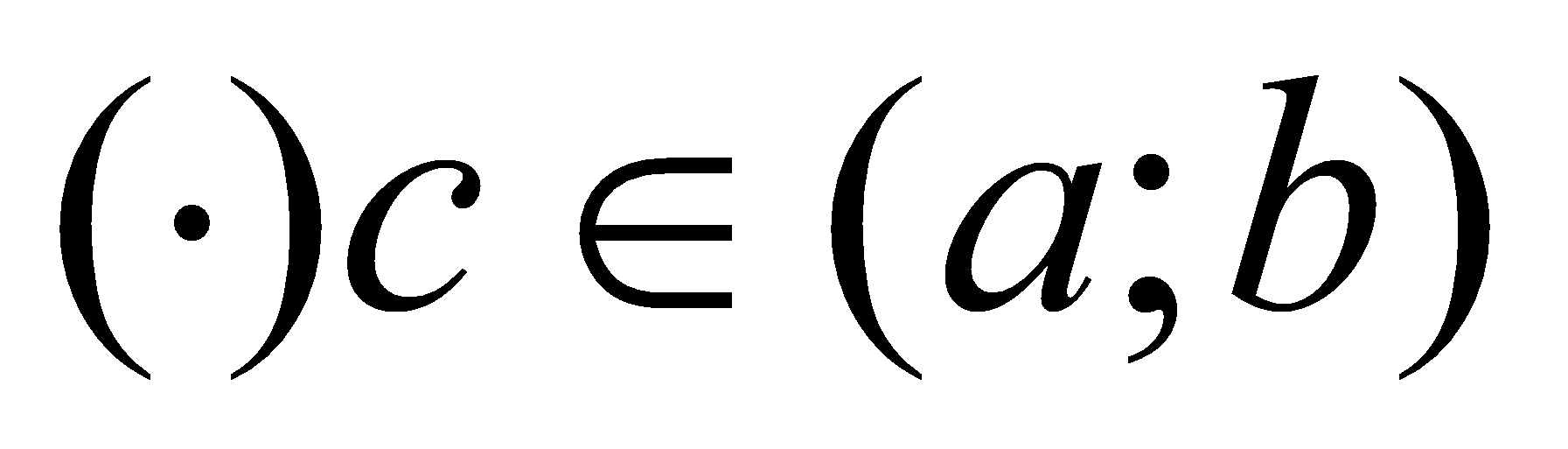 , для которой:
, для которой: 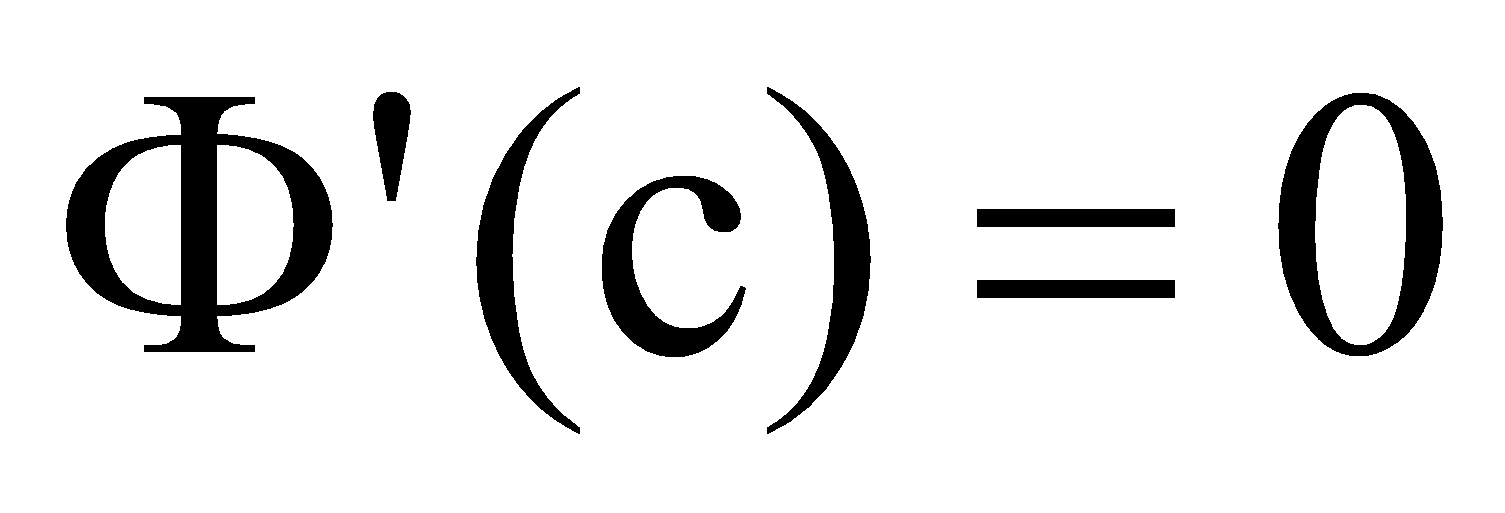 ,
, 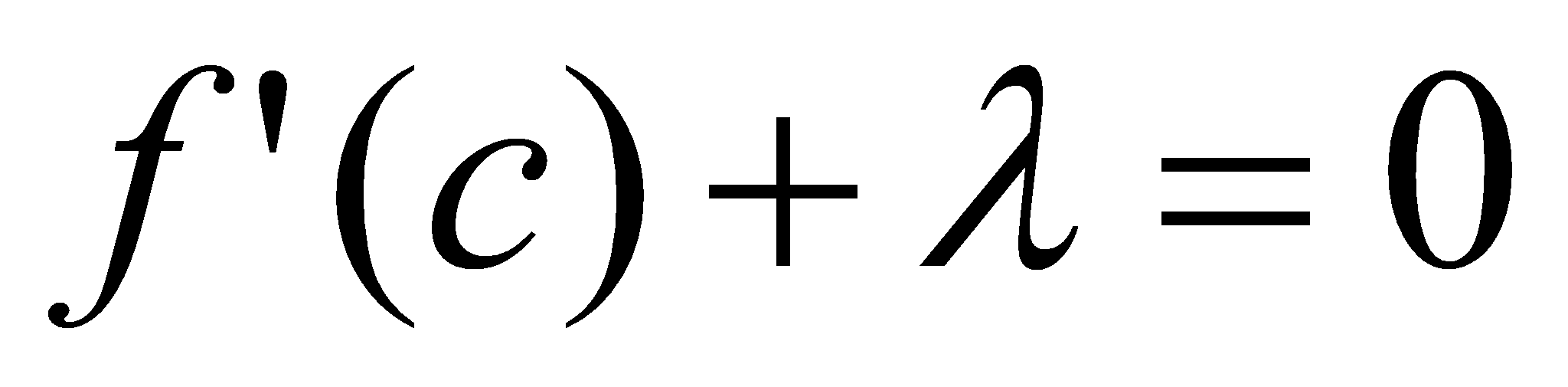 ,
,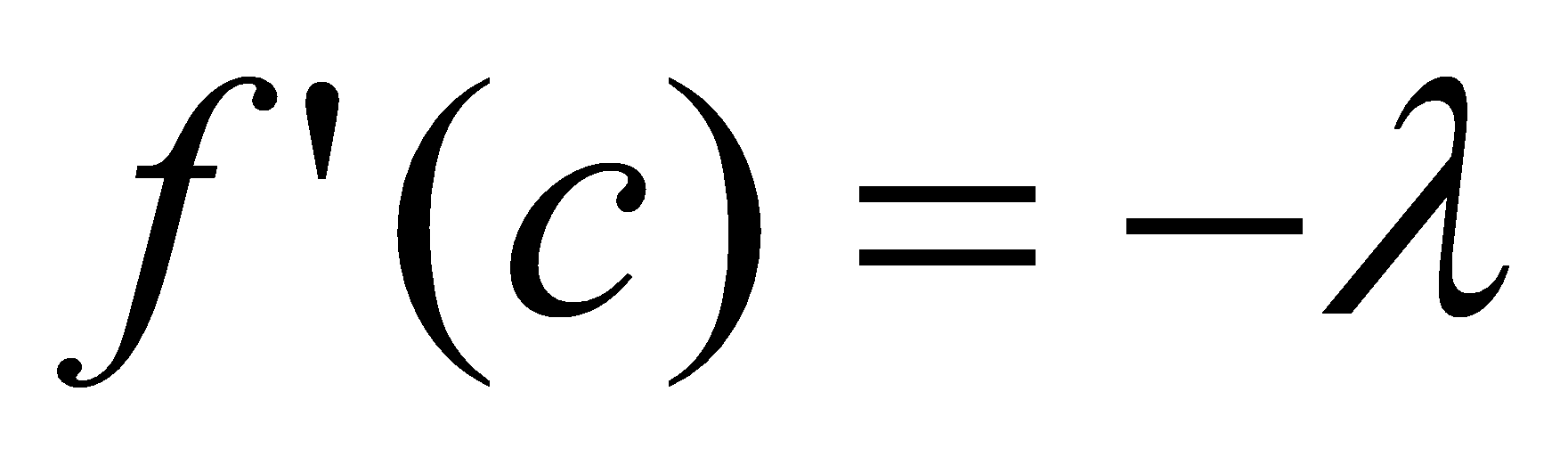 ,
,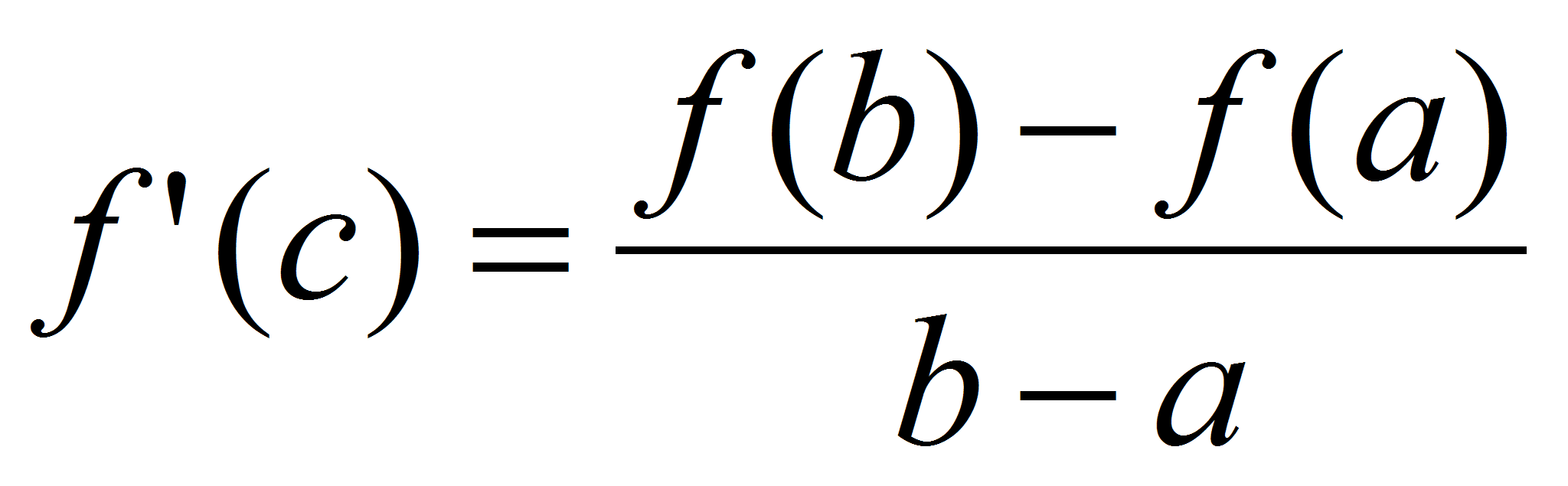 .
.
Теорема Коши:
Пусть функции 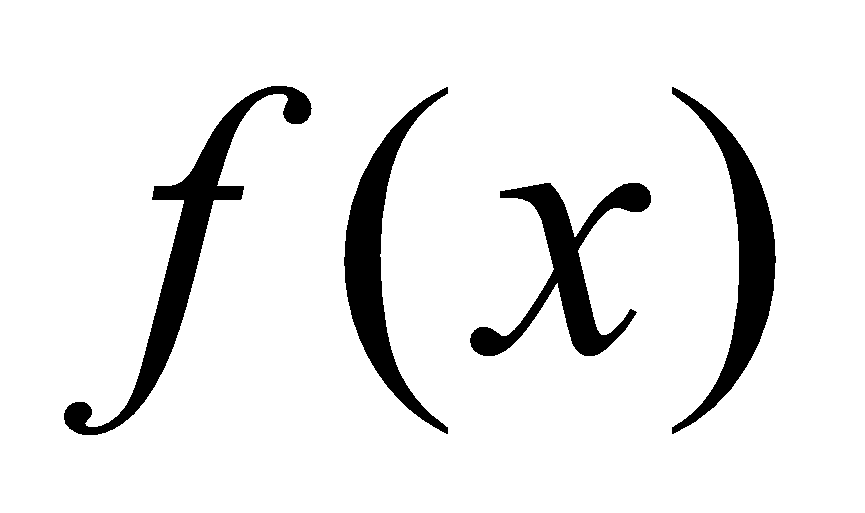 и
и 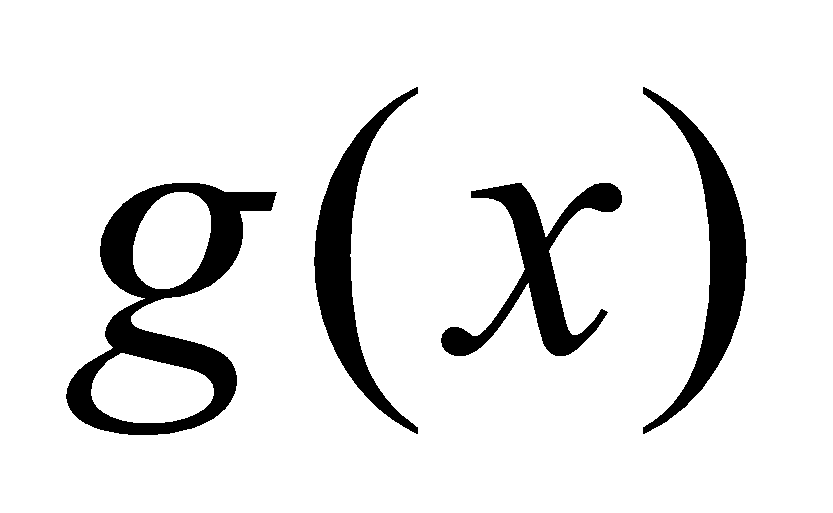 непрерывны на
непрерывны на 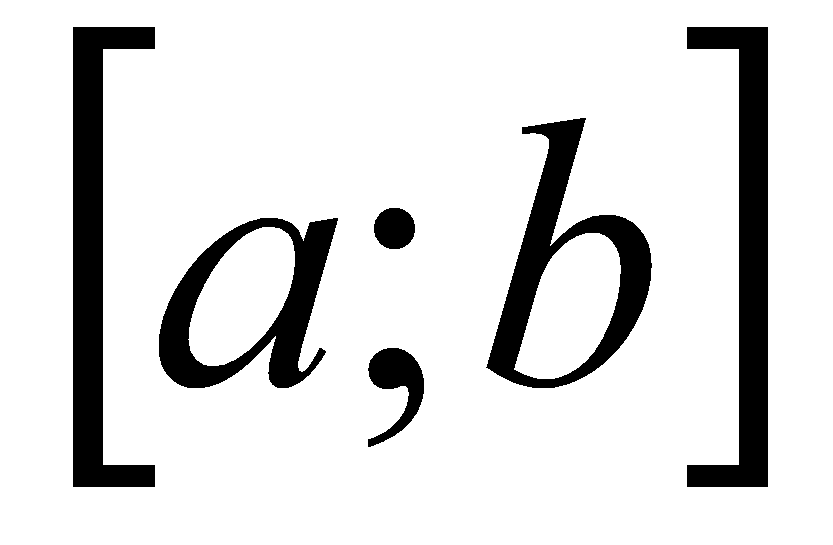 и дифференцируемы на
и дифференцируемы на 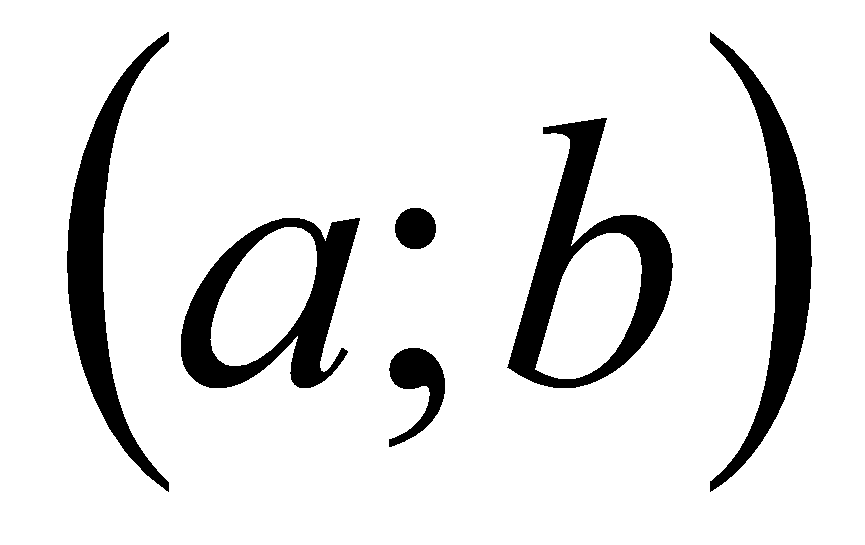 ,
, 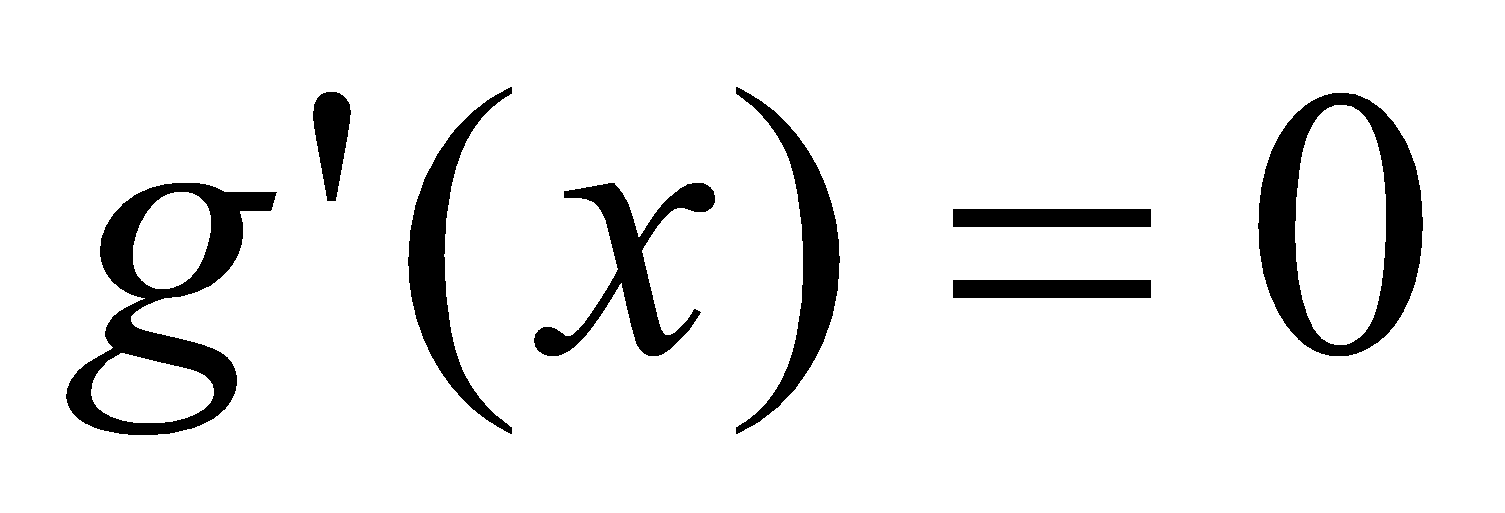 на
на 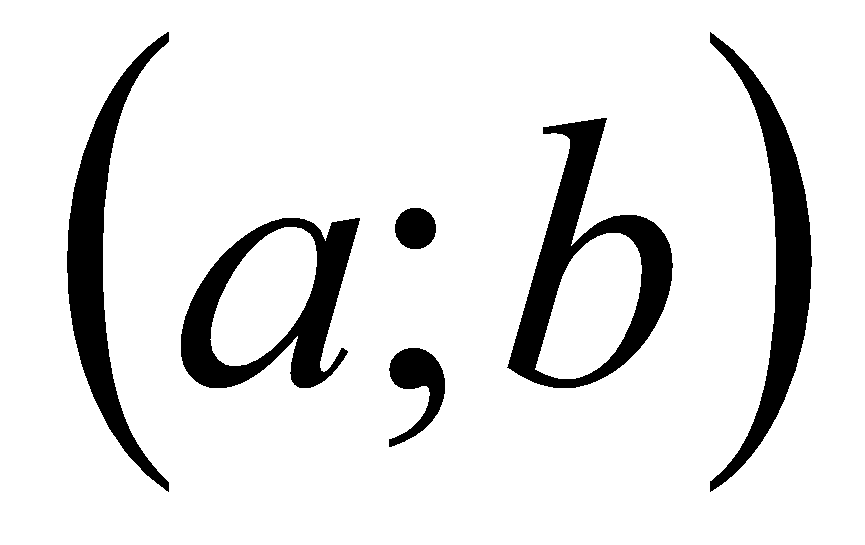 . Тогда существует хотя бы одна внутренняя точка
. Тогда существует хотя бы одна внутренняя точка 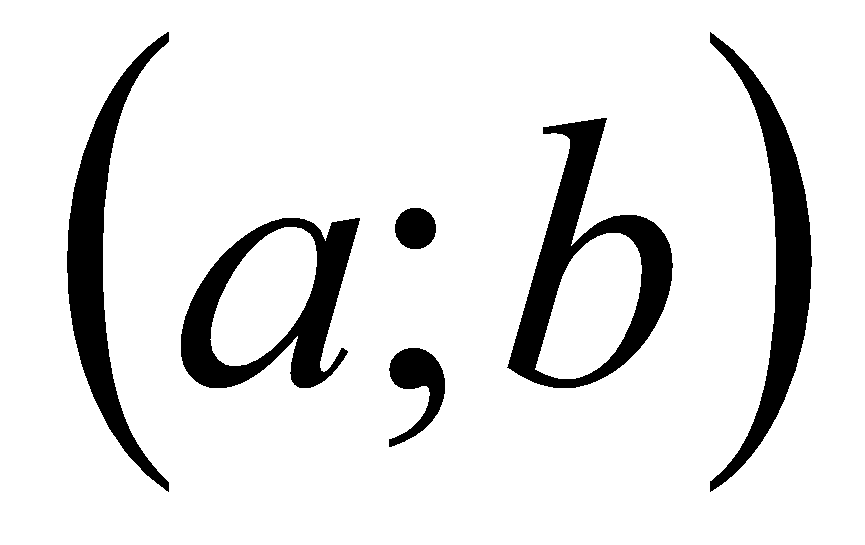 , для которой выполняется равенство
, для которой выполняется равенство 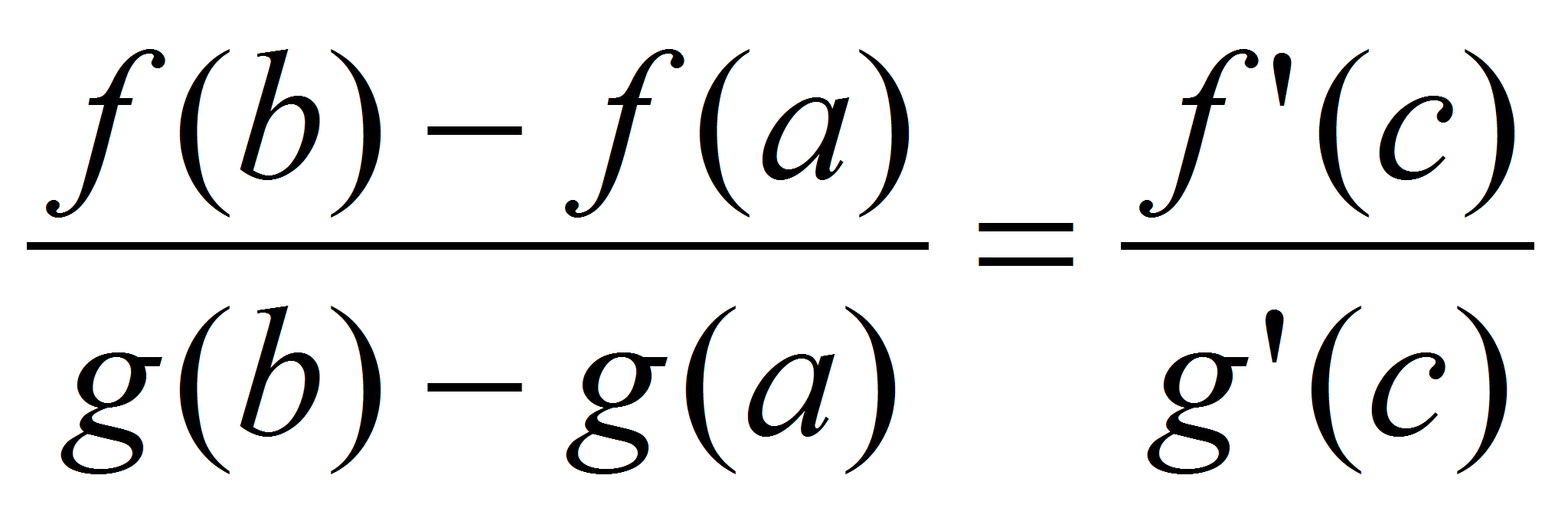 .
.
Доказательство:
Введем функцию 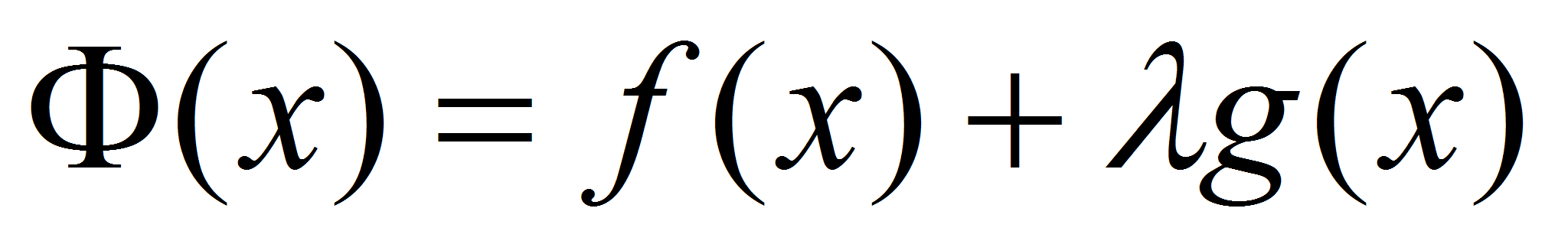 . (непрерывная на
. (непрерывная на 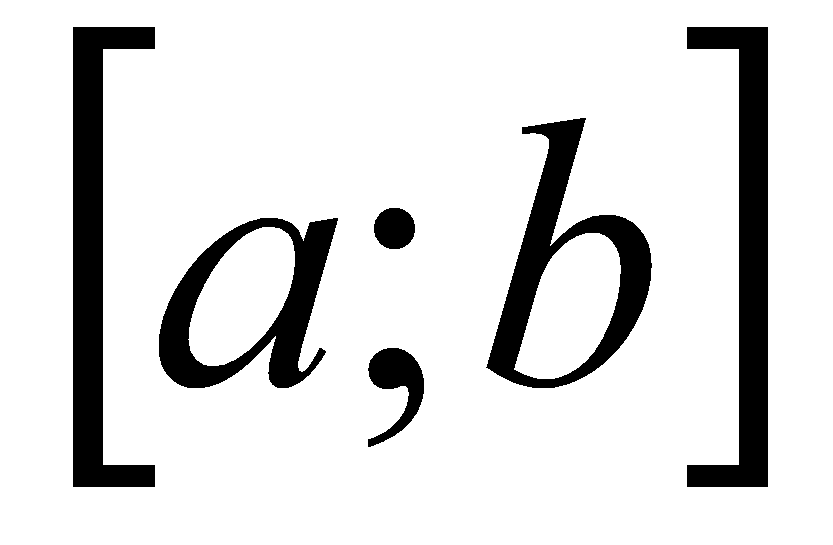 и дифференцируемая на
и дифференцируемая на 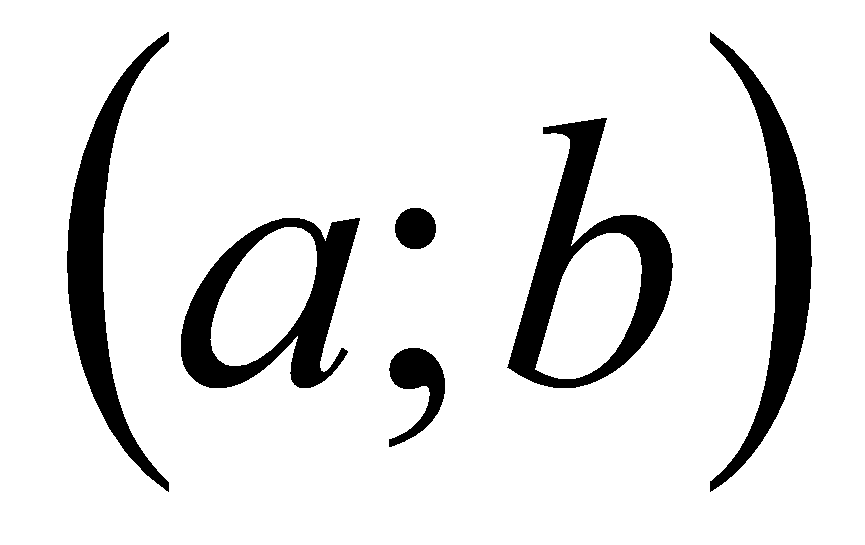 ).
).
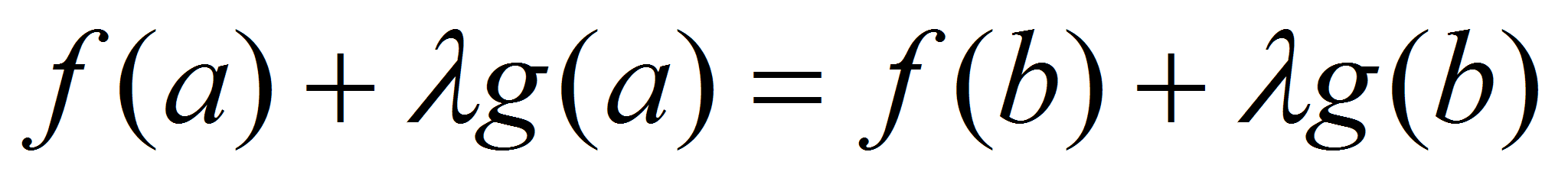
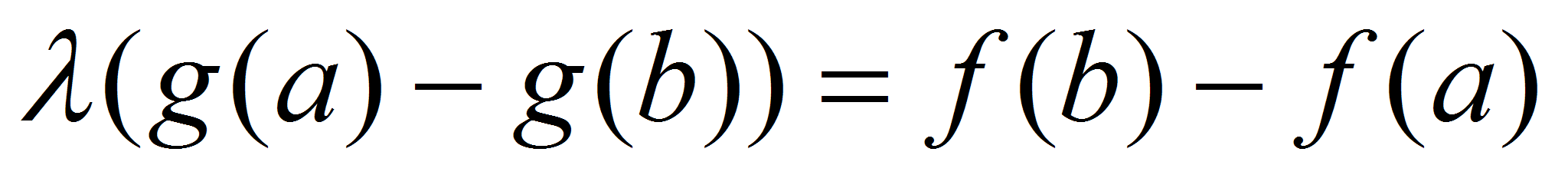
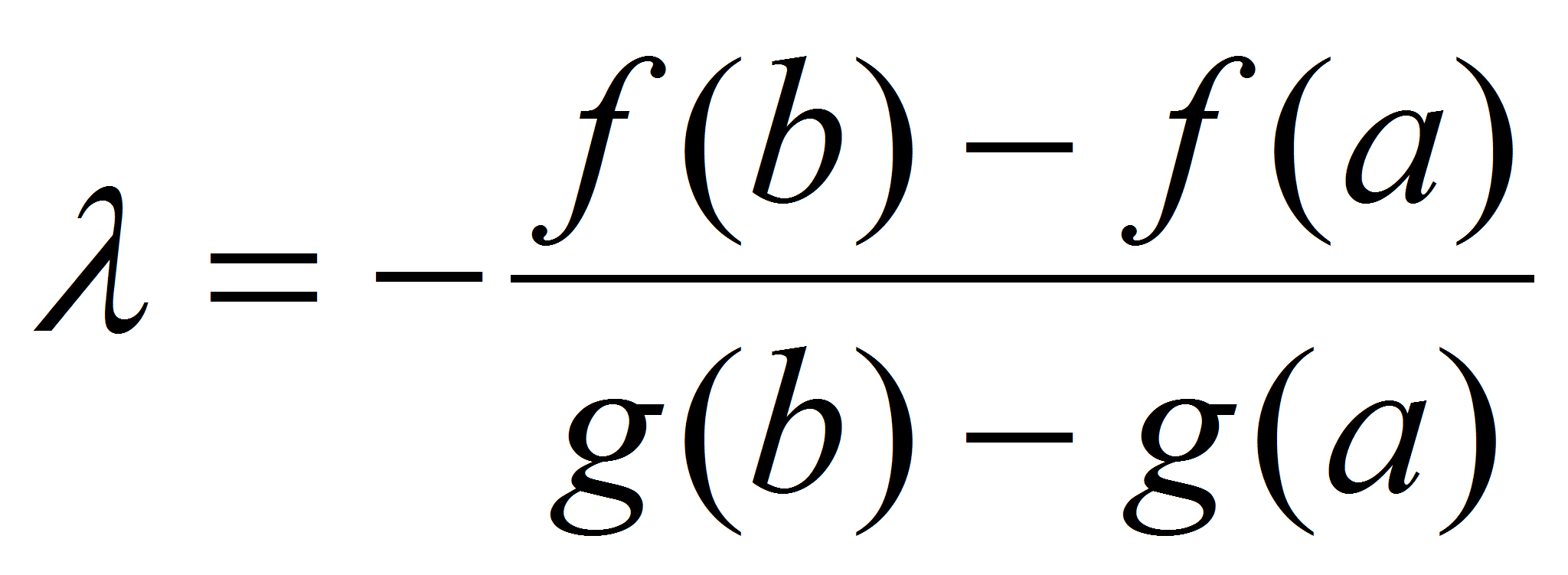
Функция 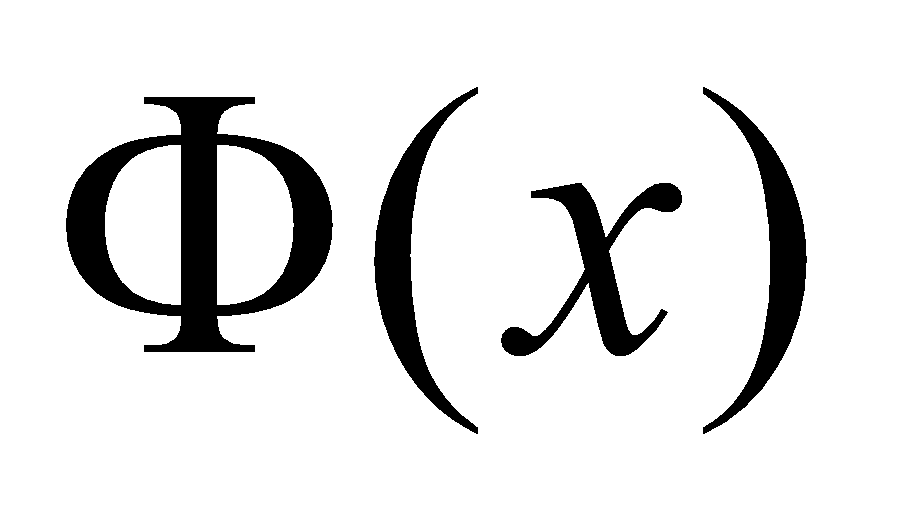 удовлетворяет Теореме Ролля
удовлетворяет Теореме Ролля  существует
существует 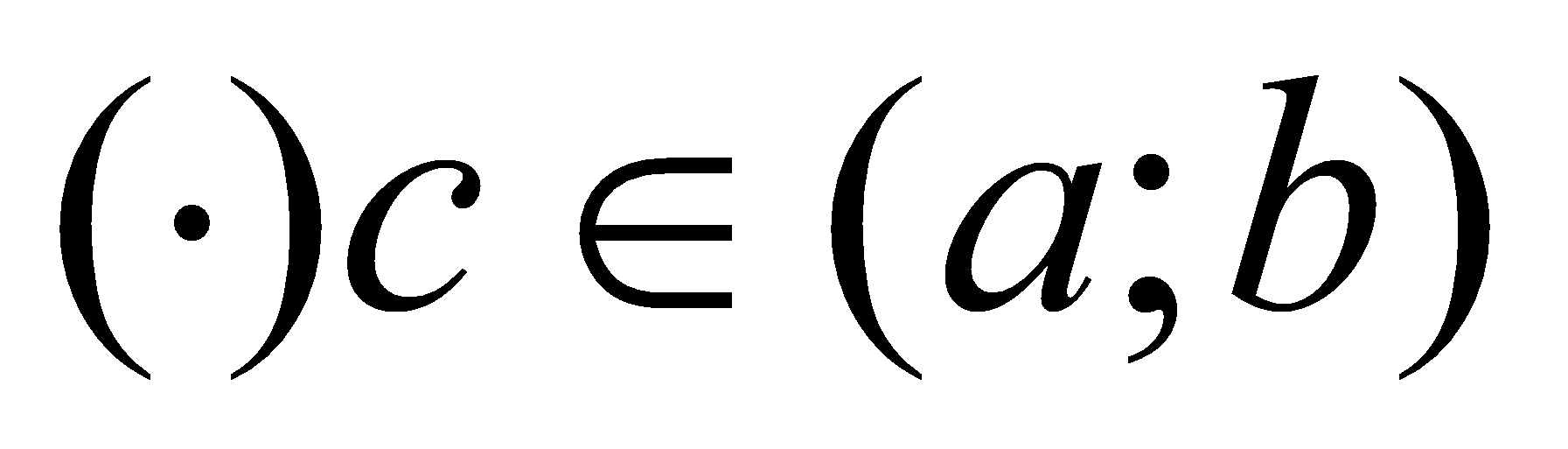 , для которой:
, для которой: 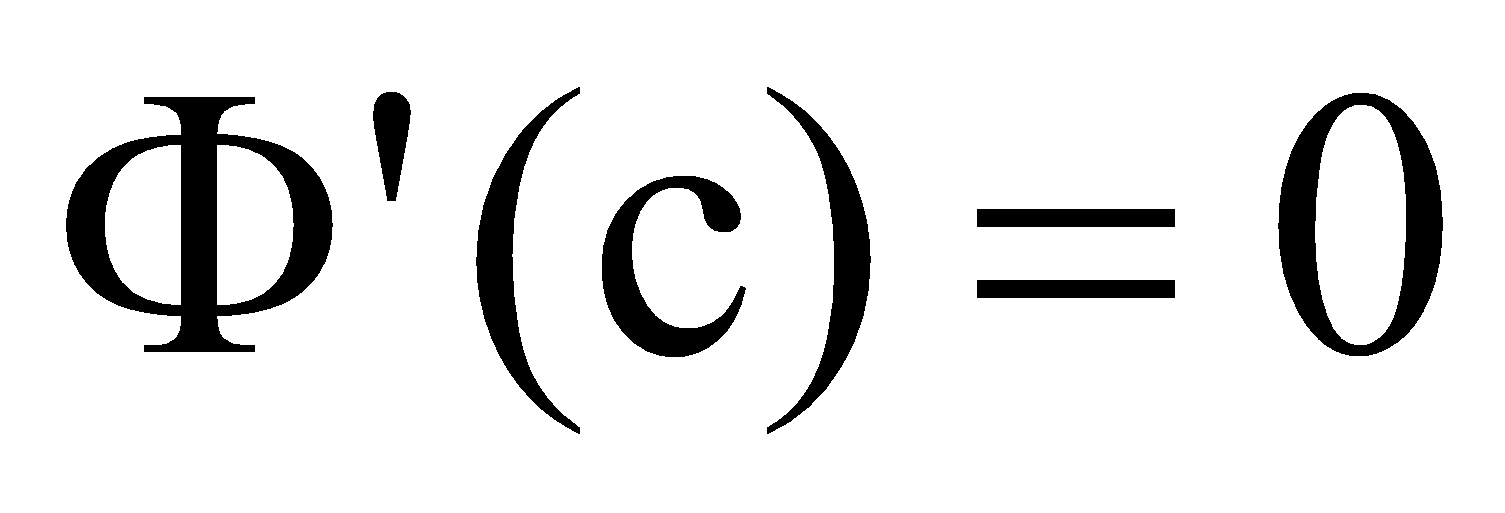 ,
, 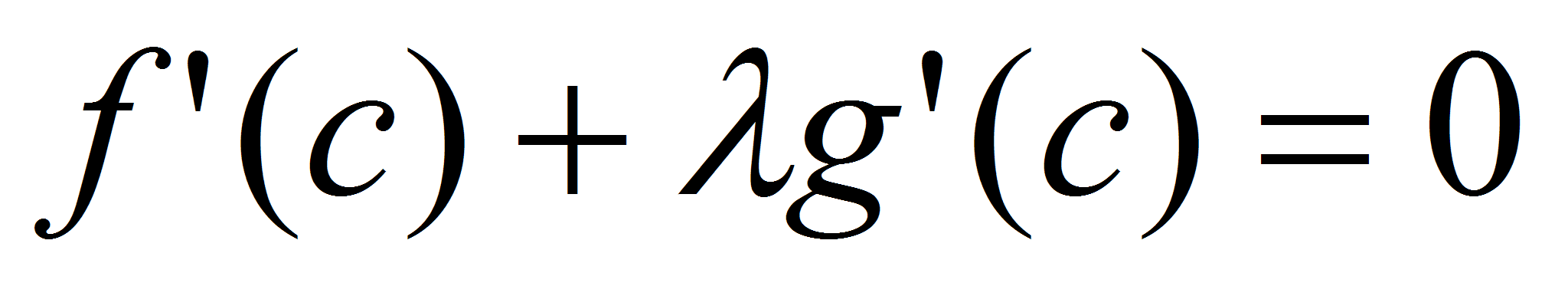 ,
,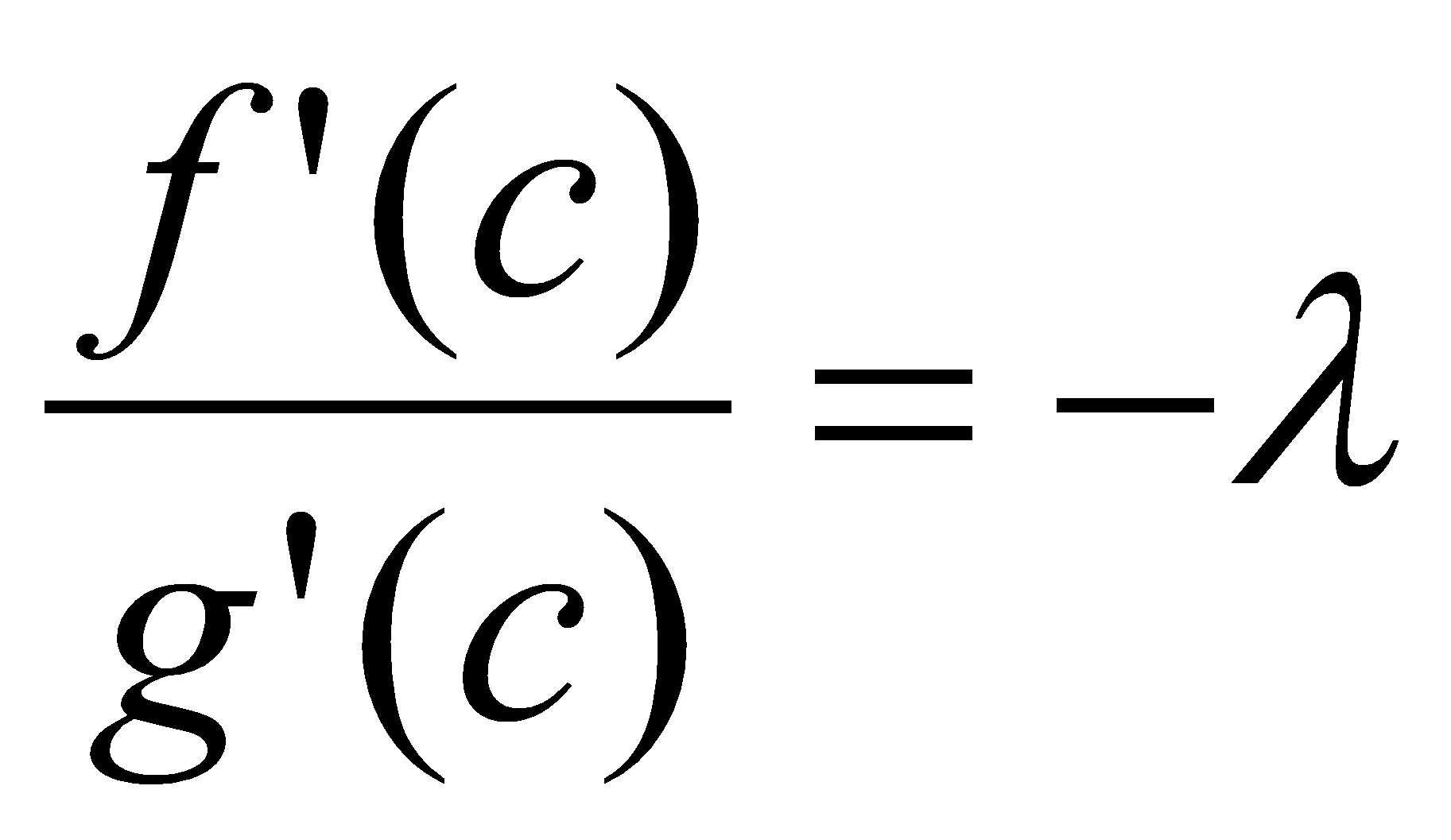 ,
,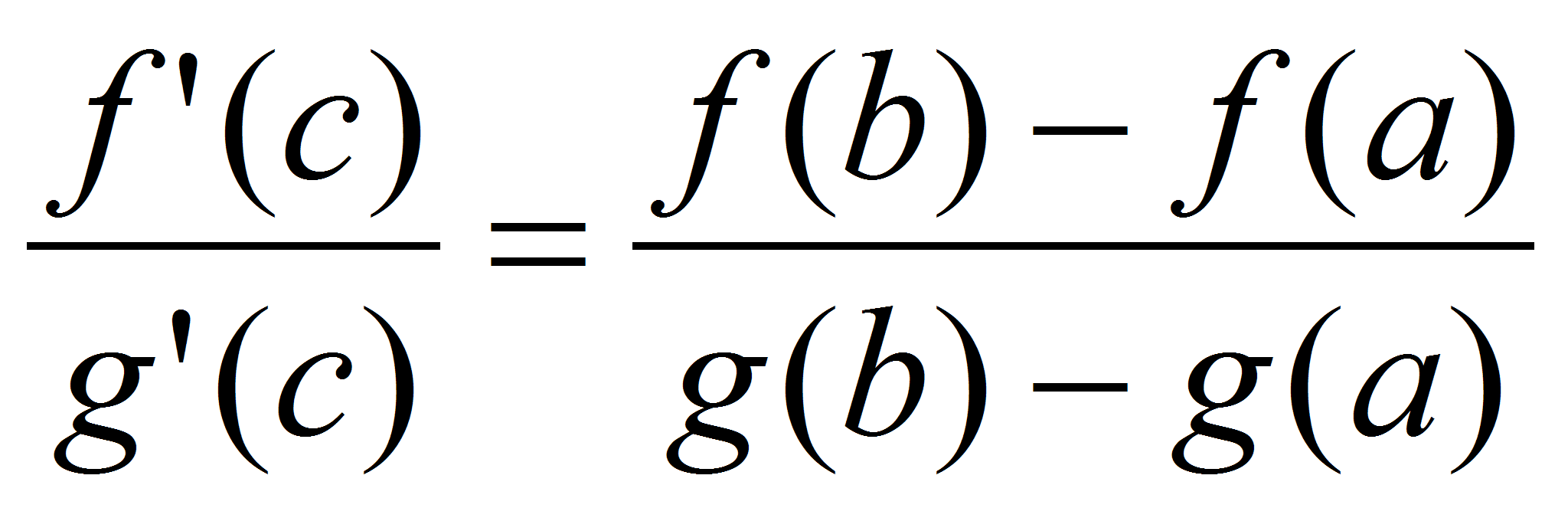 .
.

