Дифференциалом 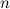 -го порядка
-го порядка 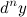 функции
функции  называется дифференциал от дифференциала
называется дифференциал от дифференциала 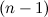 -го порядка этой функции, то есть
-го порядка этой функции, то есть
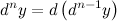
 |
|
||||||
Дифференциалы высших порядков.Дифференциалы высших порядковПусть функция
Аналогично определяются дифференциалы более высоких порядков. Определение
Дифференциалом
Получим формулы, выражающие дифференциалы высших порядков. Рассмотрим несколько случаев. Случай независимой переменнойПусть
где
Переменной является аргумент
Для вычисления дифференциала
Итак,
Рассматривая последовательно дифференциалы все более высокого порядка, получим формулу дифференциала
Случай зависимой переменнойПусть задана дифференцируемая функция
где
|
|||||||
|
|||||||