. Дифференциал функции обладает свойствами, аналогичными свойствам производной.
1. Дифференциал постоянной величины равен нулю:
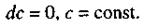 (20)
(20)
Если у = с, где с = const, то у' = 0; формула (18) принимает вид (20).
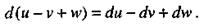 2. Дифференциал алгебраической суммы нескольких дифференцируемых функций равен такой же алгебраической сумме дифференциалов слагаемых
2. Дифференциал алгебраической суммы нескольких дифференцируемых функций равен такой же алгебраической сумме дифференциалов слагаемых
(21)
В самом деле,
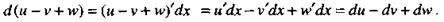 |
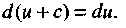 Следствие. Если две дифференцируемые функции отличаются постоянным слагаемым, то их дифференциалы равны
Следствие. Если две дифференцируемые функции отличаются постоянным слагаемым, то их дифференциалы равны
(22)
Формула (22) следует из формул (21) и (20).
3. Дифференциал произведения двух дифференцируемых функций равен произведению первой функции на дифференциал второй плюс произведение второй на дифференциал первой, т. е.
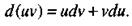 |
(23)
Действительно,
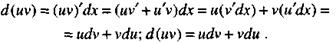 |
Следствие. Постоянный множитель можно выносить за знак дифференциала:
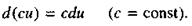 |
(24)
Формула (24) следует из формул (23) и (20).
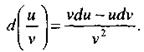 4. Дифференциал частного
4. Дифференциал частного 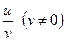 двух дифференцируемых функций и - и(х) и v = v (x) определяется формулой
двух дифференцируемых функций и - и(х) и v = v (x) определяется формулой
(25)
В самом деле,
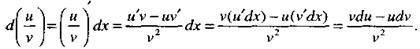 |
5. Дифференциал сложной функции (функции от функции) равен произведению производной данной функции по промежуточному аргументу на дифференциал этого промежуточного аргумента.
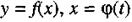 |
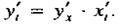
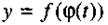 Если - дифференцируемые функции своих аргументов, то производная функции выражается формулой
Если - дифференцируемые функции своих аргументов, то производная функции выражается формулой
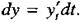 |
По определению С учетом предыдущей формулы получаем
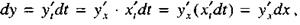 |
|||
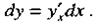 |

