Пусть у = f(и) и u = φ(х)- тогда у = f(φ{x)) — сложная функция с промежуточным аргументом и н независимым аргументом х.
 По условию
По условию 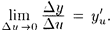 Отсюда, по теореме о связи функции, ее предела и бесконечно малой функции, имеем
Отсюда, по теореме о связи функции, ее предела и бесконечно малой функции, имеем
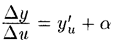 или
или 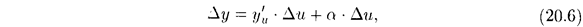 где
где 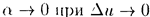 .
.
Функция u = φ(х) имеет производную в точке х: 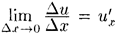 , поэтому
, поэтому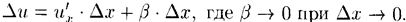 Подставив значение Δи в равенство (20.6), получим
Подставив значение Δи в равенство (20.6), получим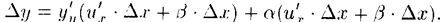 т.е.
т.е. 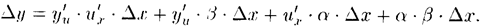 Разделив полученное равенство на Δх и перейдя к пределу при Δх→0, получим
Разделив полученное равенство на Δх и перейдя к пределу при Δх→0, получим 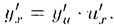
Итак, для нахождения производной сложной функции надо производную данной функции по промежуточному аргументу умножить на производную промежуточного аргумента по независимому аргументу.
Это правило остается в силе, если промежуточных аргументов несколько. Так, если у = f(u), u = φ(v), v = g{х), то 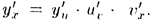 Пусть у = f(x) и х = φ(y)— взаимно обратные функции.
Пусть у = f(x) и х = φ(y)— взаимно обратные функции. Рассмотрим обратную функцию х = φ(y). Дадим аргументу у приращение Δу ≠ 0. Ему соответствует приращение Δх обратной функции, причем Δх ≠ 0 в силу строгой монотонности функции у = f(x). Поэтому можно записать
Рассмотрим обратную функцию х = φ(y). Дадим аргументу у приращение Δу ≠ 0. Ему соответствует приращение Δх обратной функции, причем Δх ≠ 0 в силу строгой монотонности функции у = f(x). Поэтому можно записать  Если Δy→0, то в силу непрерывности обратной функции приращение Δх→0. И так как
Если Δy→0, то в силу непрерывности обратной функции приращение Δх→0. И так как 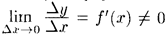 , то из (20.7) следуют равенства
, то из (20.7) следуют равенства 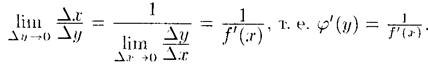
Таким образом, производная обратной функции равна обратной величине производной данной функции.
Правило дифференцирования обратной функции записывают так:

