1. Производная постоянной величины равна 0.
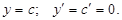
2. Производная алгебраической суммы нескольких дифференцируемых функций равна сумме производных этих функций.
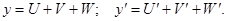
3. Производная произведения двух дифференцируемых функций равна сумме произведения каждой функции на производную другой функции.
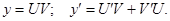
Следствия:
а) Постоянный множитель можно выносить за знак производной.
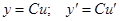
б) Производная произведения любого числа дифференцируемых функций равна сумме произведения производной каждой функции на произведение всех остальных функций.
; 
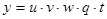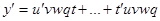
4. Производная частного равна производной числителя, умноженной на знаменатель, минус производная знаменателя, умноженная на числитель, и все это деленное на квадрат знаменателя.
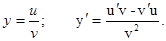
Следствия: 1)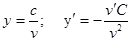 
; 2)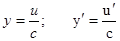 
.
2. Производная сложной и обратной функции.
1. Производная сложной функции равна произведению производных от функций, составляющих данную функцию.
, 
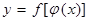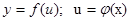- дифференцируемые функции. Тогда
.
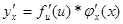2. Производная обратной функции. Пусть нам дана дифференцируемая функция y= f(x). Если y рассматривать как аргумент, а x- функцию, то новая функция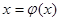 
называется обратной по отношению к y. Зная производную функции y= f(x) 
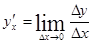, можно найти производную обратной функции 
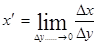, предполагая, что обратная функция существует и непрерывна.
Теорема. Для дифференцируемой функции с производной не равной 0, производная обратной функции равна обратной величине производной данной функции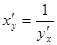 
.
Таблица производных.
| № | Функция y | Производная  |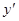
 |
||
 |
||
 |
 |
|
 |
 |
|
 |
 |
|
 |
 |
|
 |
 |
|
 |
 |
|
 |
 |
|
 |
 |
|
 |
 |
|
 |
 |
|
 |
 |
|
 |
 |
|
 |
 |
|
 |
 |
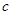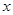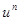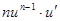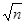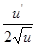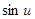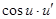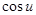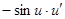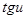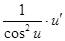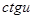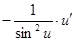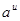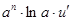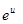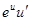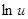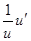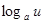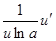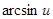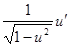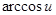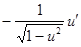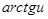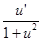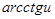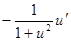