Определение.Производной функции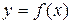 
в точке 
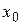называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю (если этот предел существует):
.
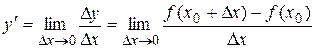Определение.Функция 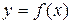, имеющая производную в каждой точке интервала 
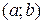, называется дифференцируемой в этом интервале.
Определение.Операция нахождения производной функции называется дифференцированием.
Значение производной функции 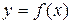в точке 
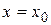обозначается одним из символов: 
.
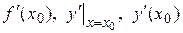Если функция 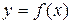описывает какой-либо физический процесс, то производная 
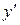есть скорость протекания этого процесса. В этом состоит физический смысл производной.
Геометрический смысл производной.Рассмотрим график непрерывной кривой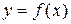 
, имеющий в точке 
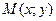невертикальную касательную. Найдем ее угловой коэффициент 
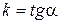, где 
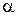- угол касательной с осью 
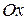. Для этого проведем через точку 
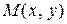и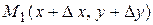 
графика секущую (рисунок 1).
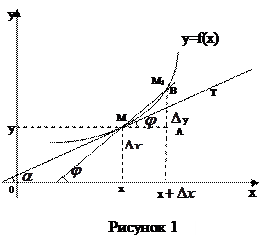Обозначим через 
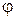- угол между секущей 
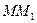и осью 
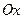. На рисунке видно, что угловой коэффициент секущей равен
.
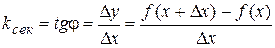При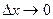 
в силу непрерывности функции приращение 
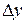тоже стремится к нулю; поэтому точка 
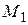неограниченно приближается по кривой к точке 
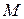, а секущая 
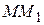, поворачиваясь около точки 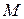, переходит в касательную. Угол 
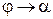, т.е. 
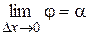. Следовательно, 
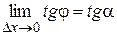, поэтому угловой коэффициент касательной равен 
.
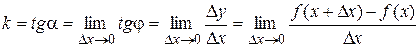Угловой коэффициент касательной к кривой
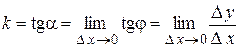. Это равенство перепишем в виде: 
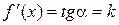, т.е. производная 
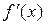в точке 
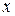равна угловому коэффициенту касательной к графику функции 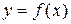в точке, абсцисса которой равна 
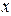. В этом заключается геометрический смысл производной.
Уравнение касательной
Пусть функция задается уравнением y=f(x), нужно написать уравнение касательнойв точке x0. Из определения производной:
y/(x)=limΔx→0ΔxΔy
Δy=f(x+Δx)−f(x).
Уравнение касательнойк графику функции: y=kx+b (k,b=const). Из геометрического смысла производной: f/(x0)=tgα=k
Т.к. x0 и f(x0)∈ прямой, то уравнение касательнойзаписывается в виде: y−f(x0)=f/(x0)(x−x0) , или
y=f/(x0)·x+f(x0)−f/(x0)·x0.
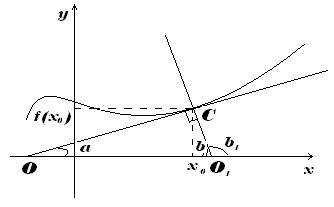
Уравнение нормали
Нормаль-- это перпендикуляр к касательной(см. рисунок). Исходя из этого:
tgβ=tg(2π−α)=ctgα=1tgα=1f/(x0)
Т.к. угол наклона нормали -- это угол β1, то имеем:
tgβ1=tg(π−β)=−tgβ=−1f/(x).
Точка (x0,f(x0))∈ нормали, уравнение примет вид:
y−f(x0)=−1f/(x0)(x−x0).
