Функция 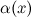 называется бесконечно малой при
называется бесконечно малой при 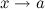 (или в точке
(или в точке 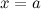 ), если
), если 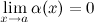
Сравнение бесконечно малых функций
Определение
Бесконечно малые функции одного порядка
Пусть 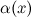 и
и 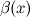 - две б.м. функции при
- две б.м. функции при 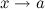 .
.
Определение
Функции 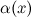 и
и 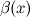 называются б.м. одного порядка малости при
называются б.м. одного порядка малости при 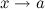 , если
, если 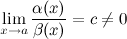
Бесконечно малые функции более низкого и высокого порядков
Определение
Если 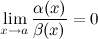 , то
, то 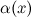 является б.м. более высокого порядка при
является б.м. более высокого порядка при 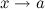 , чем
, чем 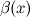 , а
, а 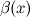 - б.м. более низкого порядка по сравнению с
- б.м. более низкого порядка по сравнению с 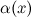 :
: 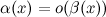 при
при 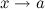 .
.
Определение
Если 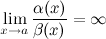 , то
, то 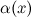 - б.м. низшего порядка малости при
- б.м. низшего порядка малости при 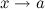 по сравнению с
по сравнению с 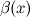 .
.
Определение
Если 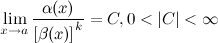 , то
, то 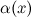 называется б.м. порядка
называется б.м. порядка 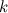 по сравнению с
по сравнению с 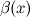 при
при 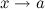 .
.
Эквивалентные (равносильные) бесконечно малые функции
Определение
Если 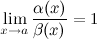 , то б.м. функции
, то б.м. функции 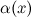 и
и 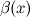 называются эквивалентными или равносильными б.м. одного порядка при
называются эквивалентными или равносильными б.м. одного порядка при 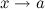 :
: 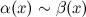 при
при 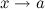 .
.
Таблица эквивалентных б.м. функций
Таблица эквивалентных б.м. функций при 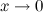
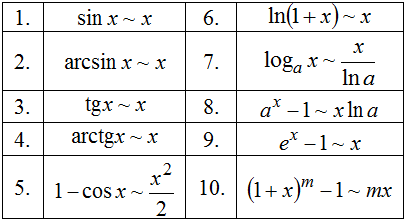
Предельные равенства для эквивалентных б.м. функций
Предел отношения двух б.м. функций 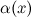 и
и 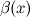 при
при 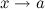 равен пределу отношения эквивалентных им б.м. функций
равен пределу отношения эквивалентных им б.м. функций 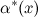 и
и 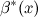 при
при 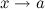 , то есть верны предельные равенства:
, то есть верны предельные равенства:
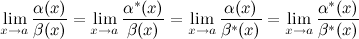
Теорема
Разность двух эквивалентных б.м. функций есть б.м. функция более высокого порядка, чем каждая из них.
Верно и обратное утверждение.
Сумма конечного числа б.м. функций разных порядков эквивалентна слагаемому низшего порядка.
Слагаемое, которое эквивалентно сумме б.м. функций, называется главной частью указанной суммы.
Замена суммы б.м. функций ее главной частью называется отбрасыванием б.м. высшего порядка.

