Теорема 1. Если функция имеет предел в точке, то этот предел единственный.
Теорема 2. Если функция имеет предел в точке, то она ограничена в некоторой проколотой окрестности этой точки.
Теорема 3. Если функция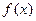 
имеет предел 
в точке 
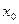, то существует проколотая окрестность точки, в которой функция 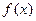имеет знак, совпадающий со знаком предела
.
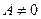Теорема 4. Если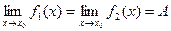 
и в некоторой проколотой окрестности точки 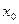имеют место неравенства 
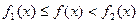, то 
.
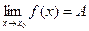Теорема 5. Пусть функци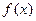и и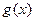 
имеют предел в точке 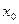. Тогда справедливы формулы:
1)
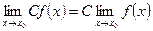, где С=const;
2) 
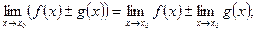
3) 
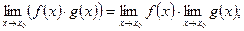
4) 
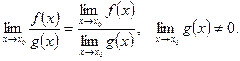
Замечание 1. Формулы суммы и произведения обобщаются на любое конечное число множителей. Если использовать их для бесконечного количества множителей, то может возникнуть ошибка.
Замечание 2. Если в результате применения формул 1) – 4) приходим к выражениям типа
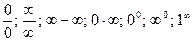
которые называют неопределенностями, то следует вначале устранить неопределенность, сделав тождественные преобразования.
Теоремы о пределах о свойствах функций, имеющих конечные пределы
ТЕОРЕМА (о единственности предела)
Пусть произвольная функция 
определена в некоторой
окрестности точки 
, 
.
Тогда если функция при 
имеет конечный предел, то он единственный, т.е.
; 
.
Доказательство методом от противного
Предположим 
. Тогда
,
в частности и при 
;
,
в частности и при .
Отсюда на 
имеем 
– неверное числовое неравенство.
Вывод: предположение о существовании не единственного
предела – ложное. Теорема доказана.
Частный случай (для последовательности)
.
Если предположить наличие двух различных пределов, то можно указать непересекающиеся окрест-ности этих пределов, в которые должны попадать одновременно ВСЕ
члены последовательности, начиная с некоторого.
ТЕОРЕМА (о локальной ограниченности функции, имеющей
при конечный предел)
: 
,
т.е. если функция при имеет конечный предел, то существует окрестность точки 
, на которой множество значений функции 
есть ограниченное числовое множество.
Доказательство. Поскольку 
к.ч., то для любого 
, в том числе для 
, существует 
так, что для 
, т.е. 
, где 
или 
.
Заметим, что обратное утверждение неверно, т.е. если функция локально ограничена на 
, то необязательно существует 
и равен конечному значению.
Контрпример. Функция 
имеет множество значений 
– ограниченное множество в любой окрестности точки 
, но 
не существует.
Заметим, что функция, имеющая в точке конечный предел, а значит, локально ограниченная в окрестности этой точки, может быть неограниченной на своей области существования. Например, 
, 
для 
.
Функция бесконечно большая при является неограниченной в любой окрестности . Обратное неверно, т.е. неограниченная в функция не обязательно бесконечно большая при . Например, 
.
Частный случай (для последовательности):
всякая сходящаяся последовательность является ограниченной, т.е.
Контрпример. 
– ограниченная последователь-ность, но не является сходящейся, поскольку ее подпосле-довательности 
и 
сходятся к несовпадающим пределам.
Итак, теорема о локальной ограниченности является "односторонней" теоремой и выражает НЕОБХОДИМОЕ условие существования конечного предела функции (и последовательности).
Следующая серия утверждений описывает связь между соотношениями для функций и их пределов.
ТЕОРЕМА (о переходе к пределу в равенстве)
Если 
на и существует , то существует 
и 
.
ПРИМЕР. Поскольку 
для 
и 
, то 
.
ТЕОРЕМА (о переходе к пределу в неравенстве)
Если 
или 
на и существуют – к.ч. и – к.ч., то 
.
Доказательство можно провести методом от противного.
Рекомендуем провести самостоятельно.
ТЕОРЕМА (о перенесении неравенства между пределами на функции)
Если существуют пределы 
и 
и выполняется неравенство 
, то существует окрестность ,
на которой .
Доказательство. Имеем
,
в частности, при 
: 
, т.е. 
. Аналогично
,
в частности, при 
, т.е. 
или 
.
Поскольку при 
, то на пересечении окрестностей 
имеем 
, т.е. указали окрестность 
, на которой характер неравенства между пределами переносится на функции.
Следствие. Если – конечное число и 
, то можно указать окрестность , на которой 
.
ТЕОРЕМА (о пределе промежуточной функции)
Если 
на и существуют и 
и их значения конечны и равны, то существует предел промежуточной функции и его значение совпадает со значением пределов оценивающих слева и справа функций.
Доказательство рекомендуем построить самостоятельно,
используя определение предела по Коши для функций и 
при .
ТЕОРЕМА (об арифметике функций, имеющих конечный предел в одной и той же точке)
Пусть функции и 
при имеют конечные пределы, т.е. 
, 
, 
и 
– конечные числа.
Тогда при имеет конечный предел каждая из функций:
1) 
; 2) 
; 3) 
(при 
).
Доказательство. 1. Операция сложения функций определяется поточечно. Утверждение верно для произвольного конечного
множества функции. Здесь рассматривается сумма двух функций.
Имеем , т.е. для всякого (в частности, для 
) существует 
так, что 
.
Аналогично ()
(
,
).
Рассмотрим и оценим: 
на .
Итак, 
, т.е. по определению предела 
– конечное
число, причем предел СУММЫ функций равен СУММЕ пределов слагаемых функций, если предел каждой слагаемой функции – конечное число.
Заметим, что обратное утверждение неверно, т.е. существование конечного предела суммы функций не определяет существование предела каждого слагаемого.
Контрпример. Пусть 
, 
, тогда 
. Но сумма функций может быть представлена слагаемыми (неоднозначно), например в виде 
и 
, и пределы слагаемых при 
не являются конечными числами (не существуют).
2. Представим 
.
Имеем – конечное число, поэтому – локально ограничена, т.е. 
.
Исходя из определения конечного предела при имеем также 
.
При 
оценивать второе слагаемое в представлении не
требуется. При расшифруем 
.
Получаем на окрестности 
, и по определению предела
.
Итак, предел ПРОИЗВЕДЕНИЯ функций равен ПРОИЗВЕДЕНИЮ пределов функций, если предел каждой функции в произведении – конечное число.
Обратное утверждение неверно.
Контрпример. Пусть 
, , тогда 
. Но произведение функций может быть представлено сомножителями неоднозначно, например 
и 
, и тогда предел сомножителя не является конечным.
