Предел функции. Геометрическая интерпритация. Второе определение предела функции.

Конечный предел функции при 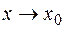. Пусть функция 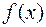определена в проколотой окрестности точки 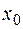, т. е. на множестве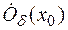 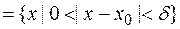. В точке 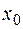значение 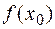может быть не определено.

Дадим определение конечного предела функции при 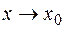на языке « 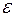— 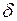» (по Коши).

Определение. Число 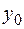называется пределом функции 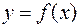в точке 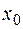(или при 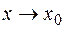), если для 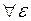>0 можно указать такое число 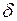( 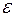)>0, что при всех 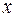, удовлетворяющих условию 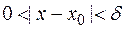, выполняется неравенство 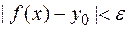, или, в более краткой записи: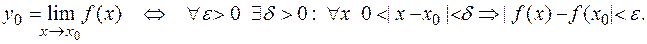

В определении используются понятия 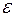-окрестности и проколотой 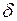-окрестности, поэтому его и называют определением на языке « 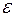— 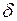» и кратко записывают так:

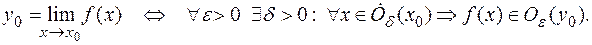
Геометрическая интерпретация определения конечного предела функции по Коши дана на рисунке.

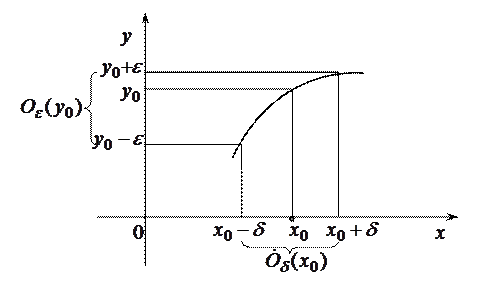
Из рисунка видно, что 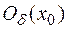отображается функцией в 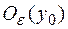, т. е. любому 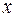из проколотой 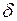-окрестности точки 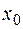соответствует значение 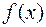, попадающее в 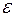-окрестность точки .

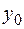Односторонние пределы функции. При рассмотрении конечного предела функции при 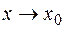предполагалось, что точка 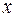, прибли­жаясь к 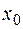, могла оставаться как слева, так и справа от нее.

Иногда приходится рассматривать предел функции 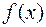при усло­вии, что точка 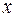, приближаясь к точке 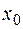, остается либо правее, либо левее ее.

Введем понятие левой и правой окрестностей точки .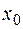

Определение. Левой 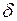-окрестностью точки 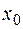(обозначается 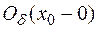) назы­вается множество всех 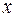, удовлетворяющих неравенству

0b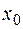

– < .

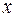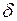Т.е. 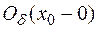= { 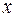| 0b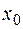

– < }.

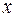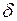Проколотая левая 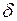-окрестность получается «выкалы­ванием» из 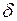-окрестности точки ,

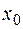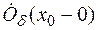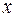= { | 0<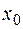

– < }.

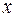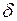Аналогично определяется и правая 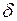-окрестность.

Определение. Число 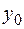называется левым пределом (левосторонним пределом или пределом слева) функции 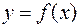в точке 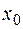, если для любого 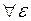> 0 существует 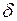= 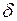( 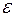)>0, такое, что для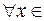

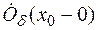
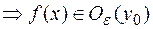
Обозначают предел слева .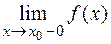

Аналогично определяется правый предел 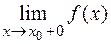функции 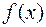в точке .

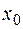Замечание. Если в точке 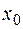функция 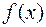имеет конечные правый и левый пределы и они равны между собой, то это число является пределом функции в точке :

= = = .

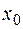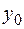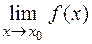
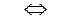
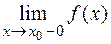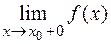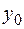Конечный предел функции при ¥.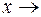

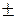Определение. Число 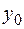называется пределом функци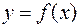и при 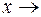+¥ , если для любого 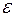>0 существует положи­тельное число 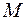, такое, что неравенство 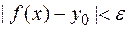выполняется для всех 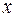, при которых > .

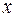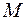Аналогично определяетcя предел и при –¥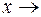

Множество { 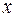| 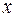> 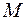} = 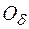(+¥) называют 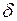-окрестностью беско­нечно удаленной точки.

Бесконечные пределы функции при 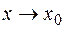. Рассмотрим случай, когда функция 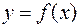при 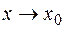по абсолютной величине неогра­ниченно возрастает. Такая функция не имеет конечного предела, поэтому необходимо обобщить понятие предела функции.

Определение.Предел функци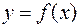и при 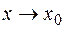назы­вается бесконечным, если для лю­бого положительного числа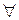 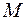>0 су­ществует число 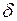> 0, такое, что для всех значений 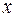, удовлетво­ряющих неравенству 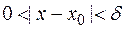, будет выполняться не­равенство | | > .

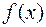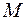Если 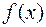стремится к беско­нечности при 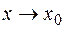, то ее называют бесконечно большой функци­ей и пишут

=¥

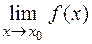Если 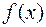стремится к бесконечности при 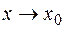и при этом принимает только положительные или только отрицательные значения, пишут соответственно:

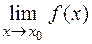=+¥ или =–¥

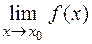Бесконечный предел функции при ¥.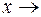

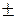Определение.Предел функци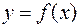и при 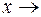+¥ (или 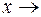–¥) называется бесконечным, если для любого сколь угодно большого числа 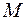найдется такое число 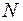> 0, что нера­венство | 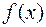| > 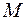выполняется для любого 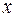, для которого | | > :

=¥

.

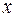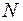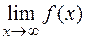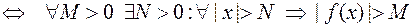
Два определения предела функции и их эквивалентность.

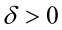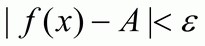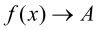а) Определение предела по Коши. Число А называется пределом функции f(x) в точке , если эта функция определена в некоторой окрестности точки , за исключением, быть может, самой точки ,и для каждого найдется число такое, что для всех x, удовлетворяющих условию , выполняется неравенство . В этом случае пишут или при .

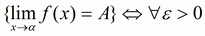
или, используя понятие окрестности, в виде

.

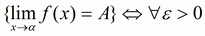
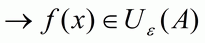Таким образом, число А есть предел функции f(x) в точке , если для любой -окрестности числа А можно найти такую проколотую -окрестность точки , что для всех x, принадлежащих этой -окрестности, соответствующие значения функции содержатся в -окрестности числа А.

б) Определение предела по Гейне. Число А называется пределом функции f(x) в точке , если эта функция определена в некоторой проколотой окрестности точки , т.е. , и для любой последовательности 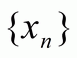, сходящейся к и такой, что для всех 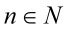, N-натуральные числа, соответствующая последовательность значений функции сходится к числу А.

в) Эквивалентность двух определений предела.

Теорема. Определения предела функции по Коши и по Гейне эквивалентны.

В определениях предела функции f(x) по Коши и по Гейне предполагается, что функция f определена в некоторой проколотой окрестности точки , т.е. существует число такое, что .

а) Пусть число А есть предел функции f в точке по Коши; тогда и

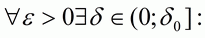
(A). (1)

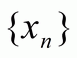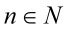Рассмотрим произвольную последовательность , сходящуюся к числу и такую, что для всех , N-натуральные числа. Согласно определению предела последовательности для найденного в (1) числа можно указать номер такой, что 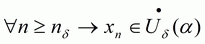, откуда в силу условия (1) следует, что 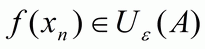. Таким образом,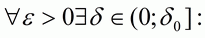 (A), (2), где , причем усл-е (2) выполняется для любой посл-ти {Xn}

такой, что и . Следовательно, , т.е. число А – предел функции f(x) в точке по Гейне.

б) Докажем, что если число А есть предел функции f(x) в точке по Гейне, то это же число является пределом функции f по Коши, т.е. выполняется условие (1). Допустим, что это неверно. Тогда 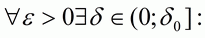. (3)

Согласно (3) в качестве можно взять любое число из полуинтервала 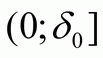. Возьмем , где 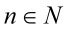, N-натуральные числа, и обозначим . Тогда в силу (3) для любого 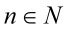, N-натуральные числа, выполняются неравенства

, (4)

. (5)

Из (4) следует, что и 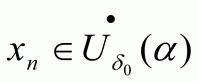при всех 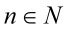, а из (5) заключаем, что число А не может быть пределом последовательности . Следовательно, число А не является пределом функции f в точке по Гейне. Полученное противоречие доказывает, что должно выполняться утверждение (1).