Монотонные последовательности. Теорема Вейерштрасса

Определение. Последовательность $\{{x_{n}\}}$ не возрастает(не убывает), если $x_{n+1}\leq x_{n}(x_{n+1}\geq x_{n})$ для $\forall n\in N$ .

Определение. Последовательность $\{{x_{n}\}}$ возрастает (убывает), если $x_{n+1}>x_{n}(x_{n+1}<x_{n})$ для $\forall n\in N$ .

Определение. Строго возрастающая или строго убывающая последовательность называется монотонной последовательностью.

Теорема. Если $\{{x_{n}\}}$ - не убывает и ограничена сверху, то она сходится. Если $\{{x_{n}\}}$ - не возрастает и ограничена снизу, то она сходится.

Доказательство. При выполнении условия теоремы последовательность $x_{n}$ ограничена.

В силу ограниченности $x_{n}\exists \inf _{n\in N}x_{n}={\underline {x}}$ , $\exists \sup _{n\in N}x_{n}={\bar {x}}$

1) Если последовательность не убывает, то $\lim _{n\to \infty }={\bar {x}}$

2) Если последовательность не возрастает, то $\lim _{n\to \infty }={\underline {x}}$

Рассмотрим первый случай.

По определению $\sup$ : $\forall \varepsilon >0\exists x_{N}:x_{N}>{\bar {x}}-\varepsilon ,x_{n}\leq {\bar {x}}0\leq -x_{N}<\varepsilon$

Т.к. $\{{x_{n}\}}$ не убывает, то при $n\leq Nx_{N}\leq x_{n}\leq {\bar {x}}$

$0<{\bar {x}}-x_{n}\leq {\bar {x}}-x_{n}<\varepsilon$ при $n\leq N$

$\forall \varepsilon >0\exists N:$ при $n\leq N|{\bar {x}}-x_{n}|<\varepsilon$ .

Второй случай рассматривается аналогично.

Принцип Кантора.

Для всякой системы вложенных отрезков существует по крайней мере одно число, которое входит в каждый из этих отрезков.

Доказательство. ►Возьмем два множества A={ 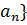и B={ 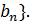Они не пусты и при любых n и m выполняется неравенство 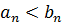.Действительно, если 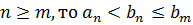. Если 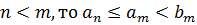. Таким образом, классы A и B удовлетворяют аксиоме непрерывности и, следовательно, существует число λ такое, что 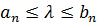для любого n, то есть λ ◄

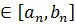Критерий Коши сходимости последовательности

Для того, чтобы последовательность имела конечный предел, необходимо и достаточно, чтобы она была фундаментальной.

Доказательство

Необходимость:

Пусть последовательность имеет конечный предел. Докажем, что она является фундаментальной.
Пусть $\exists \lim\limits_{n\to\infty}{x_n}=a$ по определению предела последовательности: $\forall \varepsilon >0 \ \exists N_\varepsilon :\forall p\geq N_\varepsilon\ |x_p-a|< \varepsilon$

Поскольку $\varepsilon$ произвольное, то мы можем взять вместо него, к примеру, $\frac{\varepsilon }{2}$ :
$p=n > N_\varepsilon\ \Bigl|x_n-a\Bigl|<\frac{\varepsilon }{2}$
$p=m > N_\varepsilon\ \Bigl|x_m-a\Bigl|<\frac{\varepsilon }{2}$
$\Bigl|x_n-x_m\Bigl|=\Bigl|(x_n-a)+(a-x_m)\Bigl|\leq\underset{\underset{\frac{\varepsilon}{2}}{\leq}}{{\underbrace{\Bigl|x_n-a\Bigl|}}} + \underset{\underset{\frac{\varepsilon}{2}}{\leq}}{{\underbrace{\Bigl|x_m-a\Bigl|}}}< \varepsilon$
То есть: $\Bigl|x_n-x_m\Bigl| < \varepsilon$ , а значит, $\{x_n\}_{n=1}^{\infty}$ — фундаментальная по определению.
Необходимость доказана.

Достаточность:

Пусть $\{x_n\}_{n=1}^{\infty}$ — фундаментальная последовательность. Докажем, что она имеет конечный предел. Сначала покажем, что $\{{x_n\}}^{\infty}_{n=1}$ — ограничена.
Поскольку $\{x_n\}_{n=1}^{\infty}$ — фундаментальная последовательность, то по определению фундаментальной последовательности:
$\forall\varepsilon > 0 \ \exists N_\varepsilon :\forall\ n > N_\varepsilon$ и $\forall\ m >N_\varepsilon$ $|x_n-x_m| < \varepsilon$

Так как $\varepsilon$ произвольное, то возьмем $\varepsilon=1 :$

$\Bigl|x_n\Bigl|=\Bigl|(x_n-x_{N\epsilon})+x_{N\epsilon}\Bigl| \leq\underset{\underset{1}{\leq}}{{\underbrace{\Bigl|x_n-x_{N\epsilon}\Bigl|}}}+\Bigl|x_{N\epsilon}\Bigl|\leq 1+ \Bigl|x_{N\epsilon}\Bigl|$
$\forall n \geq N_\varepsilon: |x_n|<(1+|x_{N\epsilon}|)=const=C$ $\Bigl|x_n\Bigl|\leq C$
$C=\max\{1+\Bigl|x_{N\epsilon}\Bigl|;\Bigl|x_1\Bigl|,\Bigl|x_2\Bigl|,...,\Bigl|x_{N\varepsilon-1}\Bigl|\} \Rightarrow$
$\Rightarrow \forall n \epsilon \mathbb{N} : \Bigl|x_n\Bigl|\leq C \Rightarrow$
$\{x_n\}_{n=1}^{\infty}$ — ограничена.

По теореме Больцано-Вейерштрасса последовательность $\{x_n\}_{n=1}^{\infty}$ имеет сходящуюся подпоследовательность $\{{x_{n_k}\}}^{\infty}_{k=1}$

Пусть $\lim\limits_{k\rightarrow\infty}{x_{n_k}}=a$ , покажем, что число aa и будет пределом всей последовательности $\{{x_n\}}^{\infty}_{n=1}$ :
Поскольку $\{x_n\}_{n=1}^{\infty}$ фундаментальная:
$\forall \varepsilon>0\ \exists n_\varepsilon : \forall n,m > n_\varepsilon$ $|x_n-x_m| <\frac{\varepsilon}{2}$

Так как $\{x_{n_k}\}_{k=1}^{\infty}$ сходящаяся:
$\lim\limits_{k\rightarrow\infty}{x_{n_k}}=a : \forall \varepsilon>0\ \exists k_\varepsilon :\forall n_k \geq n_{k_\varepsilon}$
$|x_{n_k}-a|<\frac{\varepsilon}{2}$
$\forall \varepsilon>0 : |x_n-a|=|(x_n-x_{n_k})+(x_{n_k}-a)|\leq |x_n-x_{n_k}|+|x_{n_k}-a|<\varepsilon$
Возьмём $N_\varepsilon = \max\{n_\varepsilon, n_{k_\varepsilon}\}$ , тогда: $\forall \varepsilon >0\ \exists\ N_\varepsilon : \forall n\geq N_\varepsilon : |x_n-a|<\frac{\varepsilon}{2}+\frac{\varepsilon}{2}=\varepsilon$

Достаточность доказана.

Монотонные последовательности. Теорема Вейерштрасса. Принцип Кантора. Критерий Коши.

Монотонные последовательности. Теорема Вейерштрасса

Критерий Коши сходимости последовательности

Доказательство

Необходимость:

Достаточность: