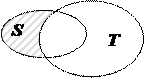Под множеством понимается любая (конечная или бесконечная) совокупность объектов с некоторой общей характеристикой (или, что то же самое - объектов одинаковой природы). Эти объекты, как вам известно еще со школы, называются элементами множества. Множества с конечным числом различных элементов могут быть описаны путем явного перечисления всех этих элементов: обычно, эти элементы заключаются в фигурные скобки. Например, 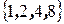 - множество степеней двойки, заключенных между 1 и 10. Как правило, множество обозначается прописной буквой какого - либо алфавита, а его элементы - строчными буквами того же или другого алфавита. Для некоторых особо важных множеств приняты стандартные обозначения, которых стоит придерживаться. Так, буквами
- множество степеней двойки, заключенных между 1 и 10. Как правило, множество обозначается прописной буквой какого - либо алфавита, а его элементы - строчными буквами того же или другого алфавита. Для некоторых особо важных множеств приняты стандартные обозначения, которых стоит придерживаться. Так, буквами
N - множество натуральных чисел
Z - множество целых чисел
Q - множество рациональных чисел
R - множество вещественных (или действительных) чисел
При заданном множестве S включение 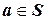 указывает на то, что a - элемент множества S; в противном случае, как вы знаете, пишут
указывает на то, что a - элемент множества S; в противном случае, как вы знаете, пишут 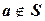 (или
(или 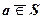 ).
).
Множество можно описать, указав свойство, присущее только элементам именно этого множества. Множество всех объектов, обладающих свойством 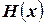 , обозначают через
, обозначают через 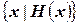 . Например:
. Например: 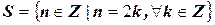 - множество всех четных чисел;
- множество всех четных чисел; 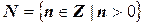 - множество натуральных чисел.
- множество натуральных чисел.
Множество, не содержащее элементов, называется пустым и его принято обозначать символом Æ.
Говорят, что S – подмножество множества 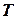 или
или 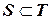 (
(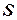 содержится в
содержится в 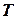 ), если все элементы множества
), если все элементы множества 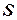 являются также элементами множества
являются также элементами множества 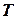 , то есть
, то есть
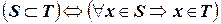 .
.
Два множества 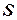 и
и 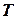 совпадают (или равны), если у них одни и те же элементы. Символически это выглядит так:
совпадают (или равны), если у них одни и те же элементы. Символически это выглядит так:
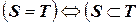 и
и 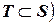 .
.
Заметим, что пустое множество Æ (т.е. множество совсем не содержащее элементов) по определению входит в число подмножеств любого множества.
Если 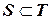 , но
, но 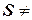 Æи
Æи 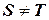 , то
, то 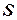 - называется собственным подмножеством в
- называется собственным подмножеством в 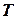 . Для выделения подмножества
. Для выделения подмножества 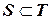 часто используют какое - либо свойство, присущее только элементам из
часто используют какое - либо свойство, присущее только элементам из 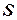 .
.
Для множеств 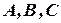 справедливы следующие соотношения:
справедливы следующие соотношения:
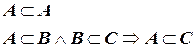
( значок 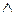 - это значок конъюнкции, т. е. логическое «и»).
- это значок конъюнкции, т. е. логическое «и»).
Конечное множество называется упорядоченным, если каждому элементу этого множества поставлено в соответствие некоторое число (номер элемента) от 1 до 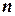 .
.
Операции над множествами.
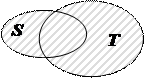
Для пояснения некоторых определений и свойств операций над множествами и различных соотношений между ними воспользуемся диаграммами Эйлера – Венна, на которых множества, подлежащие рассмотрению, изображаются в виде совокупности точек на плоскости.
1. Под пересечением (произведение) двух множеств 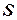 и
и 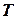 понимается множество:
понимается множество:
|
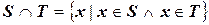
Например:
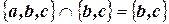
2. Под объединением (сумма) двух множеств 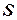 и
и 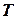 понимается множество :
понимается множество :
|
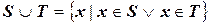
(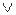 - значок дизъюнкции, логическое «или»)
- значок дизъюнкции, логическое «или»)
Например:
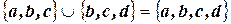
3. Разностью 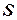 \
\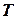 множеств
множеств 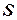 и
и 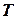 называется совокупность тех элементов, из
называется совокупность тех элементов, из 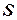 , которые не содержатся в
, которые не содержатся в 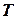 , то есть
, то есть
|
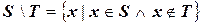
Порядок множеств при выполнении этой операции существенен.
4. Если 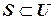 (здесь
(здесь 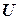 – основное , универсальное множество) то
– основное , универсальное множество) то 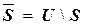
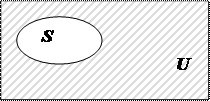 |
будем называть дополнением множества 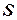 относительно
относительно 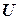 (обозначается также:
(обозначается также: 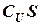 ).
).
Можно еще много говорить о множествах, их свойствах, операциях над ними и т.п. Остановлюсь лишь на некоторых свойствах, указанных операций, после чего перейдем к новому разделу. Итак, для множеств 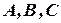 справедливы следующие соотношения:
справедливы следующие соотношения:
1. Свойство коммутативности: 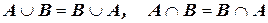 ;
;
2. Свойство дистрибутивности: 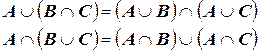
3. Свойство ассоциативности: 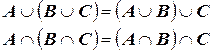
4. 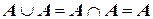
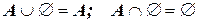 ;
;
5. 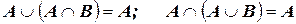 ;
;
6. 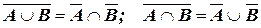 ;
;
7. 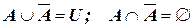 ;
;
8. 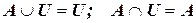 и т.д.
и т.д.
Числовые множества.
Множества могут состоять из объектов самой различной природы. Их элементами могут быть буквы, атомы, числа, уравнения, точки, углы и т.д. Именно этим объясняется чрезвычайная широта теории множеств и ее приложимость к самым разнообразным областям знания (математика, физика, лингвистика, экономика и т.д.). Для математики особо важную роль играют множества, составленные из "математических" объектов – чисел, геометрических фигур и т.д. Очень часто встречаются числовые множества, т.е. множества, элементами которых являются числа. Примерами числовых множеств являются:
а) множество всех натуральных чисел ( 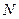 );
);
б) множество всех положительных рациональных чисел ( 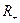 );
);
в) множество всех рациональных чисел( 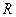 );
);
г) множество всех целых чисел ( 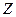 );
);
д) множество всех чисел, удовлетворяющих неравенству 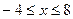 ;
;
е)  множество всех чисел вида
множество всех чисел вида 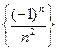 , где n принимает все натуральные значения.
, где n принимает все натуральные значения.
Некоторые числовые множества имеют особые названия. Если даны два числа a и b, a<b, то множество всех чисел, удовлетворяющих неравенству 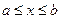 , называют числовым отрезком или, если это не вызывает недоразумений, просто отрезком и обозначают [a; b]. На числовой оси ему соответствует отрезок с концами a и b (см. рис. 3).
, называют числовым отрезком или, если это не вызывает недоразумений, просто отрезком и обозначают [a; b]. На числовой оси ему соответствует отрезок с концами a и b (см. рис. 3).
Множество чисел, удовлетворяющих неравенству 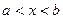 , называют числовым промежутком или, короче, промежутком и обозначают (a, b). На числовой оси это множество изображается отрезком, у которого отброшены концевые точки (см. рис. 4).
, называют числовым промежутком или, короче, промежутком и обозначают (a, b). На числовой оси это множество изображается отрезком, у которого отброшены концевые точки (см. рис. 4).
Иногда нам будут встречаться множества чисел, удовлетворяющих неравенствам 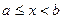 или
или 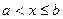 (рис. 5). Их называют (числовыми) полуотрезками и обозначают [a; b), или (a; b]. Квадратная скобка означает, что соответствующий конец включается в множество, а круглая, что он исключается.
(рис. 5). Их называют (числовыми) полуотрезками и обозначают [a; b), или (a; b]. Квадратная скобка означает, что соответствующий конец включается в множество, а круглая, что он исключается.
Числовые отрезки, полуотрезки и промежутки имеют конечную длину. Рассмотрим теперь множество чисел, удовлетворяющих неравенству 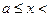 +∞. Такое множество называется числовым лучом. Числовой луч имеет бесконечную длину. Числовым лучом называют и множество чисел, удовлетворяющее неравенству вида –∞
+∞. Такое множество называется числовым лучом. Числовой луч имеет бесконечную длину. Числовым лучом называют и множество чисел, удовлетворяющее неравенству вида –∞ 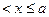 .
.
Числовые лучи обозначают так: [a; +∞), (–∞;a].
С числовыми множествами приходится иметь дело при решении уравнений и неравенств. С каждым уравнением связаны два числовых множества. Первое из них – область определения уравнения. Это множество состоит из всех значений x, для которых имеют смысл обе части уравнения. Например, область определения уравнения
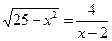
задается условиями 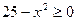 (квадратный корень в множестве действительных чисел можно извлечь лишь из неотрицательного числа) и
(квадратный корень в множестве действительных чисел можно извлечь лишь из неотрицательного числа) и 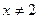 (на нуль делить нельзя). Отсюда получаем, что область определения данного уравнения состоит из всех точек числового отрезка [-5, 5], кроме точки x=2.
(на нуль делить нельзя). Отсюда получаем, что область определения данного уравнения состоит из всех точек числового отрезка [-5, 5], кроме точки x=2.
Второе множество, связываемое с уравнением, – это множество его корней, т.е. чисел, при подстановке которых в уравнение оно обращается в тождество.
Например, для данного уравнения множество корней состоит из одного числа 3
Если каждый элемент множества В является в то же время элементом множества А, то говорят, что В – подмножество в А, и пишут 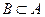 . Каждое непустое множество имеет по крайней мере два подмножества: пустое множество Ø и само множество А. Таким образом, пустое множество является подмножеством любого множества.
. Каждое непустое множество имеет по крайней мере два подмножества: пустое множество Ø и само множество А. Таким образом, пустое множество является подмножеством любого множества.
Приведем примеры подмножеств:
а) числовой отрезок [–1, 3] есть подмножество числового отрезка
[–4; 5];
б) множество всех квадратов есть подмножество множества всех прямоугольников;
в) множество Z всех целых чисел есть подмножество множества Q всех рациональных чисел;
г) множество точек треугольника, вписанного в круг, есть подмножество множества точек этого круга;
д) множество точек круга является подмножеством множества точек описанного вокруг него квадрата;
е) множество звезд нашей Галактики является подмножеством множества всех звезд Вселенной;
ж) множество учеников восьмого класса данной школы есть подмножество множества всех учеников этой школы. В свою очередь множество учеников этой школы является подмножеством множества всех школьников в Республики Беларусь;
з) множество жителей Москвы является подмножеством множества всех жителей России;