Соответствия. Свойство соответствий.

Соответствие – способ задания взаимосвязей, взаимодействий между элементами множества (наряду с отношениями). Частными случаями соответствий являются функции, отображения, преобразования, операции и др.

Соответствием между множествами А и В (рис. 1.7) называется некоторое подмножество G их декартова произведения: .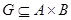

Если 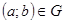, то говорят, что 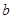соответствует а при соответствии .

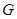Область определения 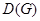соответствия G – множество пр₁G={а:(а,b) ÎG}. Область значений 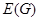соответствия G - множество пр₂G={b:(а,b) ÎG}.

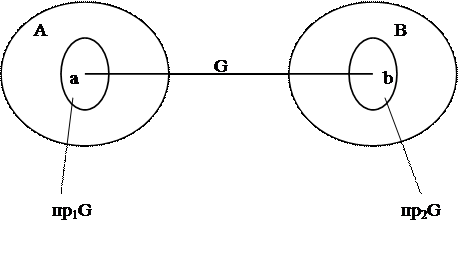Рис. 1.7. Соответствие G между множествами А и B

В принятых обозначениях, каждый элемент 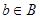, соответствующий данному элементу 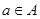называется образом 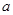при соответствии 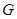, наоборот, элемент 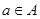называется прообразом элемента 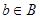при данном соответствии.

Свойства соответствий :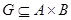

1) Соответствие называется полностью определённым, если 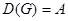, то есть каждый элемент множества 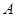имеет хотя бы один образ во множестве 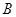; в противном случае соответствие называется частичным.

2) Соответствие 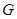называется сюръективным, если 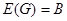, то есть если каждому элементу множества 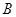соответствует хотя бы один прообраз во множестве .

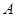3) Соответствие 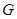называется функциональным (однозначным), если любому элементу множества 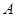соответствует единственный элемент множества .

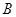4) Соответствие называется инъективным, если оно является функциональным, и при этом каждый элемент множества 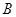имеет не более одного прообраза.

5) Соответствие 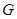называется взаимнооднозначным (биективным), если любому элементу множества 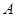соответствует единственный элемент множества 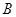, и наоборот. Можно сказать также, что соответствие является взаимнооднозначным, если оно является полностью определённым, сюръективным, функциональным, и при этом каждый элемент множества 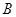имеет единственный прообраз.