1. Декартово произведение множеств
Используя две цифры, например, 3 и 5, можно записать четыре двузначных числа: 35, 53, 33 и 55. Несмотря на то, что числа 35 и 53 записаны с помощью одних и тех же цифр, эти числа различные. В том случае, когда важен порядок следования элементов, в математике говорят об упорядоченных наборах элементов. В рассмотренном примере мы имели дело с упорядоченными парами.
Упорядоченную пару, образованную из элементов aиb, принято записывать, используя круглые скобки: (a;b). Элементaназываютпервой координатой (компонентой) пары, а элементb–второй координатой (компонентой) пары.
Пары (а; b) и (с;d) равны в том и только том случае, когда а = с иb=d.
В упорядоченной паре (а; в) может быть, что а = в. Так, запись чисел 33 и 55 можно рассматривать как упорядоченные пары (3; 3) и (5; 5).
Упорядоченные пары можно образовывать как из элементов одного множества, так и двух множеств.
Пример
Даны множества А=1,2,3, В=3,5. Образовать упорядоченные пары так, чтобы первая компонента принадлежала множеству А, а вторая – множеству В.
Перечислив все такие пары, получим множество: (1; 3), (1; 5), (2; 3), (2; 5), (3;3), (3;5).
Видим, что имея два множества А и В, мы получили новое множество, элементами которого являются упорядоченные пары чисел. Это множество называют декартовым произведением множеств А и В.
Определение. Декартовым произведением множеств А и В называется множество всех пар, первая компонента которых принадлежит множеству А, а вторая компонента принадлежит множеству В.
Декартово произведение множеств А и В обозначают А. Используя это обозначение, определение произведения можно записать так:
х; у) х и у .
Пример
Найти декартово произведение множеств А и В, если:
а) А = m, p, e, f, k; b) A = B=3, 5.
Решение. а) Действуем согласно определению – образуем все пары, первая компонента которых выбирается из А, а вторая – из В: А (m; p); (m; f); (m; k); (p; e); (p; f);(p; k).
b) Декартово произведение равных множеств находят, образуя всевозможные пары из элементов данного множества: А А = (3; 3); (3; 5); (5; 3); (5; 5).
Упорядоченная пара 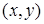 – это объект, в котором указаны первый и второй элементы (соответственно,
– это объект, в котором указаны первый и второй элементы (соответственно, 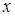 и
и 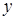 ). Декартовым произведением
). Декартовым произведением 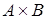 двух множеств
двух множеств 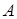 и
и 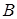 называется множество всех упорядоченных пар с первым элементом из множества
называется множество всех упорядоченных пар с первым элементом из множества 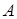 и со вторым элементом из множества
и со вторым элементом из множества 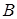 :
:
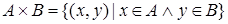 .
.
Если 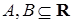 , то декартово произведение
, то декартово произведение 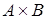 представляется на координатной плоскости: пара
представляется на координатной плоскости: пара 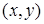 изображается точкой с координатами
изображается точкой с координатами 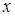 и
и 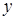 .
.

