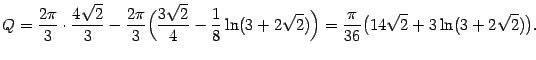Если дуга кривой, заданная неотрицательной функцией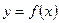 
, 
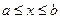, вращается вокруг оси Ox, то площадь поверхности вращения вычисляется по формуле 
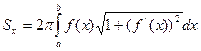, где a и b — абсциссы начала и конца дуги.
Если дуга кривой, заданная неотрицательной функцией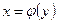 
, 
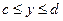, вращается вокруг оси Oy, то площадь поверхности вращения вычисляется по формуле
,
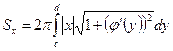где с и d — абсциссы начала и конца дуги.
Если дуга кривой задана параметрическими уравнениями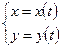 
, 
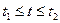, причем 
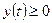, то
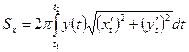
Если дуга задана в полярных координатах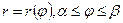 
, то
.
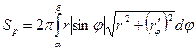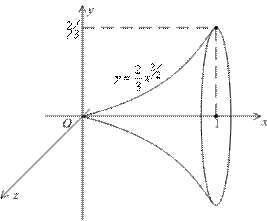
Пример. Вычислим площадь поверхности, образованной вращением в пространстве вокруг оси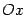 
части линии y= 
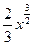, расположенной над отрезком 
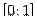оси .
Так как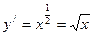 
, то формула даёт нам интеграл
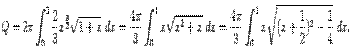
Сделаем в последнем интеграле замену t=x+(1/2) и получим:
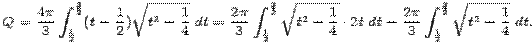
В первом из интегралов правой части сделаем замену z=t2-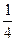 
:
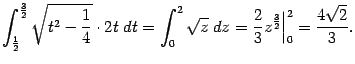
Для вычисления второго из интегралов в правой части обозначим его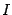 
и проинтегрируем по частям, получив уравнение для :
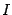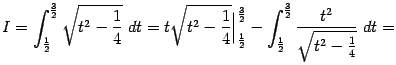
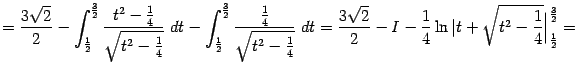
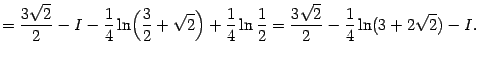
Перенося 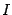в левую часть и деля на 2, получаем
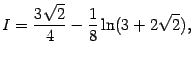
откуда, наконец,
