Введем функцию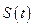 
, равную длине переменной дуги от точки 
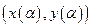до 
.
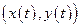Рассмотрим промежуток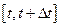 
. Приращение 
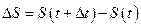равно длине дуги, заданной на отрезке 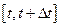. Запишем оценку для приращения длины 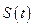на этом промежутке:
.
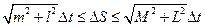есь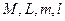 
, соответственно, наибольшие и наименьшие значения модулей производных 
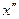и 
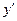на отрезке 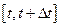. Из непрерывности производных вытекает, что
.
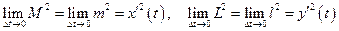То есть
.
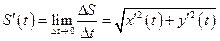ким образом, длина переменной дуги – дифференцируемая функция, и по формуле Ньютона-Лейбница ее приращение на отрезке 
равно
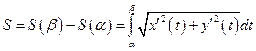. (1)
Пример 1. Найти длину одной арки циклоиды
.
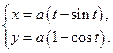
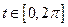Решение: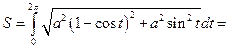 
.
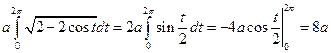