Пусть в полярной системе координат дана кривая, уравнение которой 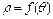 , где
, где 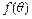 - непрерывная функция при
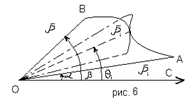
- непрерывная функция при 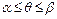 . Требуется вычислить площадь криволинейного сектора, ограниченного радиусами – векторами ОА и ОВ (для которых соответственно
. Требуется вычислить площадь криволинейного сектора, ограниченного радиусами – векторами ОА и ОВ (для которых соответственно
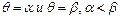 )
)
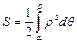 .
.
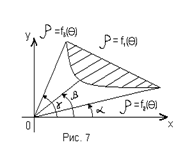 Если плоская фигура ограничена несколькими кривыми, уравнения которых заданы в полярных координатах, то вычисления площади такой фигуры стараются свести к вычислению алгебраической суммы площадей криволинейных секторов.
Если плоская фигура ограничена несколькими кривыми, уравнения которых заданы в полярных координатах, то вычисления площади такой фигуры стараются свести к вычислению алгебраической суммы площадей криволинейных секторов.
Следовательно, будем иметь
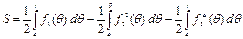 . (т.е. из площади криволинейного сектора, ограниченного
. (т.е. из площади криволинейного сектора, ограниченного 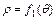 , отнимаем площади криволинейных секторов, ограниченных линиями
, отнимаем площади криволинейных секторов, ограниченных линиями 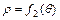 ,
, 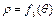 )
)

