До сих пор мы рассматривали определенный интеграл с постоянными пределами интегрирования 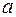 и
и 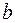 . Если оставить постоянным нижний предел интегрирования
. Если оставить постоянным нижний предел интегрирования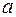 , а верхний
, а верхний 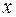 изменять так, чтобы
изменять так, чтобы 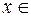
 , то величина интеграла будет изменяться. Интеграл вида
, то величина интеграла будет изменяться. Интеграл вида
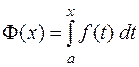
называется определенным интегралом с переменным верхним пределом и является функцией верхнего предела 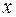 . Здесь для удобства переменная интегрирования обозначена буквой
. Здесь для удобства переменная интегрирования обозначена буквой 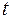 , а верхний предел интегрирования — буквой
, а верхний предел интегрирования — буквой 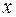 .
.
С геометрической точки зрения, функция 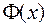 в случае
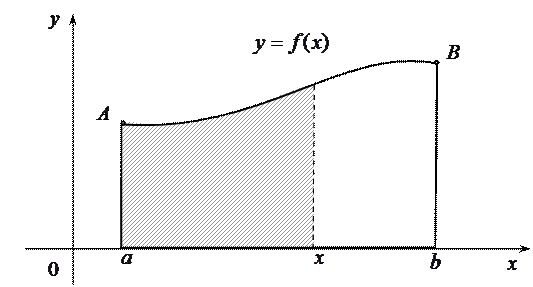
в случае 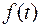 r0 представляет собой площадь заштрихованной на рисунке криволинейной трапеции.
r0 представляет собой площадь заштрихованной на рисунке криволинейной трапеции.
Найдем производную от 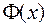 по
по 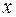 , т. е. производную определенного интеграла по верхнему пределу.
, т. е. производную определенного интеграла по верхнему пределу.
Теорема.Производная определенного интеграла от непрерывной функции  no его переменному верхнему пределу существует и равна подынтегральной функции, в которой вместо переменной интегрирования подставлено значение верхнего предела:
no его переменному верхнему пределу существует и равна подынтегральной функции, в которой вместо переменной интегрирования подставлено значение верхнего предела:
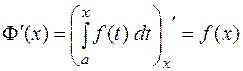 .
.
Доказательство. Возьмем любую точку 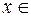
 и придадим ей приращение
и придадим ей приращение 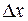 так, чтобы
так, чтобы 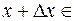
 . Тогда
. Тогда
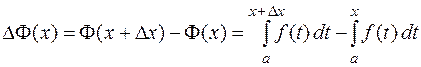 .
.
Используя аддитивность определенного интеграла, имеем
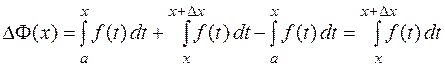 .
.
Применяя теорему о среднем, получаем
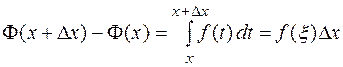 ,
,
где 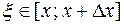 .
.
По определению производной, учитывая, что функция непрерывна, получим:
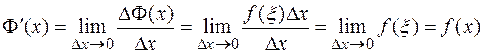 .
.
⊠
Из теоремы следует, что определенный интеграл с переменным верхним пределом 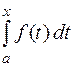 является первообразной для подынтегральной функции
является первообразной для подынтегральной функции  на отрезке
на отрезке  .
.
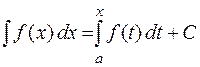 ,
,
т. е. установлена связь между неопределенным и определенным интегралами.
Так как интеграл 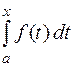 существует для любого значения
существует для любого значения 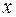 ,то данная теорема является одновременно и теоремой о существовании первообразной у каждой непрерывной функции
,то данная теорема является одновременно и теоремой о существовании первообразной у каждой непрерывной функции  . Этой первообразной может быть определенный интеграл с переменным верхним пределом.
. Этой первообразной может быть определенный интеграл с переменным верхним пределом.

