Теорема 3. Пусть функция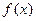 
непрерывна на отрезке 
.
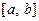Если:
1) функция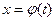 
и ее производная 
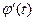непрерывны при 
;
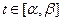2) множеством значений функции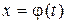 
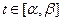при является отрезок ;
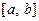3) 
, 
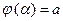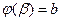, то справедлива формула
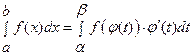. (4)
Формула (3) называется формулой замены переменной в определенном интеграле.
Заметим, что:
1. При вычислении определенного интеграла методом подстановки, использование замены переменной позволяет упростить исходный интеграл, приблизив его к табличному. При этом нет необходимости возвращаться к исходной переменной интегрирования – достаточно лишь найти новые пределы интегрирования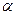 
и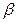 
(для этого надо решить относительно переменной t уравнения 
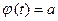и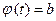 
)).
2. Часто вместо подстановки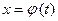 
используют подстановку 
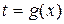. В этом случае нахождение новых пределов интегрирования по переменной t упрощается: 
, 
.
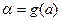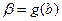3. Не следует забывать менять пределы интегрирования при замене переменных.
