Теорема 4. Функция, непрерывная на отрезке, интегрируема на нем.  Если функция f непрерывна на отрезке [a,b], то она, во-первых, ограничена на нем, а во-вторых, равномерно непрерывна. Последнее означает, что для любого
Если функция f непрерывна на отрезке [a,b], то она, во-первых, ограничена на нем, а во-вторых, равномерно непрерывна. Последнее означает, что для любого  > 0 существует такое
> 0 существует такое 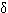 > 0 , что для всех точек x
> 0 , что для всех точек x  [a,b] и x'
[a,b] и x'  [a,b] таких, что |x - x'| <
[a,b] таких, что |x - x'| < 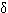 , выполняется неравенство | f(x') - f(x)| <
, выполняется неравенство | f(x') - f(x)| <  .
.
Возьмем для отрезка [a,b] какое-либо разбиение 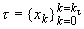 мелкости |
мелкости | | <
| < 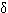 . Тогда для любых двух точек x и x', принадлежащих одному и тому же отрезку разбиения
. Тогда для любых двух точек x и x', принадлежащих одному и тому же отрезку разбиения  , x
, x  [xk-1,xk], x'
[xk-1,xk], x'  [xk-1,xk], имеет место неравенство|x - x'| < xk-1 - xk =
[xk-1,xk], имеет место неравенство|x - x'| < xk-1 - xk = 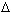 xk < |
xk < | | <
| < 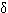 , а поэтому и неравенство | f(x') - f(x)| <
, а поэтому и неравенство | f(x') - f(x)| <  . Отсюда следует, что колебание
. Отсюда следует, что колебание  k(f) функции f на отрезке [xk-1,xk] удовлетворяет неравенству
k(f) функции f на отрезке [xk-1,xk] удовлетворяет неравенству
|
|
(23.27) |
Следовательно,
|
|
(23.28) |
Поскольку  было произвольным положительным числом, то неравенство (23.28) означает, что
было произвольным положительным числом, то неравенство (23.28) означает, что 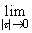
 = 0 . Поэтому в силу следствия 1 теоремы 2 функция f интегрируема на отрезке [a,b].
= 0 . Поэтому в силу следствия 1 теоремы 2 функция f интегрируема на отрезке [a,b]. 
Теорема 5. Функция, монотонная на отрезке, интегрируема на нем.  Пусть для определенности функция f возрастает на отрезке [a,b]. Тогда, в частности, для любого x
Пусть для определенности функция f возрастает на отрезке [a,b]. Тогда, в частности, для любого x  [a,b] выполняется неравенство
[a,b] выполняется неравенство
f(a) < f(x) < f(b),
и, следовательно, функция f ограничена на отрезке [a,b]. Очевидно также, что в силу возрастания функции f для любого разбиения 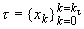 отрезка [a,b] имеют место равенства
отрезка [a,b] имеют место равенства
|
mk = |
(23.29) |
|
Mk = |
Поэтому, заметив, что xk-1 - xk
|
xk-1 - xk = |
(23.30) |
и что x0 = a, 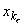 = b получим
= b получим
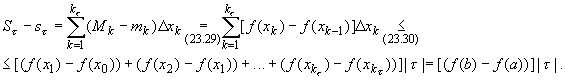
Отсюда следует, что 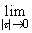 (
(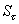 -
- 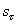 ) = 0 , и потому, согласно теореме 2, функция f интегрируема на отрезке [a,b].
) = 0 , и потому, согласно теореме 2, функция f интегрируема на отрезке [a,b]. 
Замечание. Отметим, что монотонные на отрезке функции могут быть и разрывными. Так, например, функция f(x) = sign x монотонна и разрывна на любом отрезке, содержащем точку x = 0. Поскольку же всякая монотонная функция, в частности, f(x) = sign x, согласно теореме 4, интегрируема, то отсюда следует, что существуют разрывные интегрируемые функции.


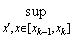 | f(x') - f(x)| <
| f(x') - f(x)| < 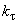 .
.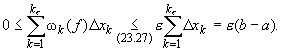
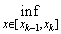 = f(x) = f(xk-1),
= f(x) = f(xk-1),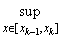 = f(x) = f(xk).
= f(x) = f(xk).