Пусть функция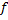 
, определённая на отрезке 
, ограничена на этом отрезке и пусть 
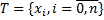- разбиение отрезка , 
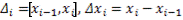(i=1,n). Обозначим
, 
,
, 
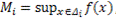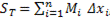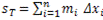. (5)
Назовём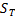 
и 
соответственно верхней и нижней суммами Дарбу для функции 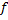при заданном разбиении 
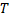отрезка . Заметим, что эти суммы не зависят от выборки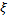 
. Рассмотрим свойства сумм Дарбу.
С в о й с т в о 1. Для любой выборки 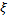справедливы неравенства
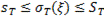. (6)
○ Так как для любого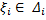 
, выполняются неравенства
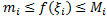
то
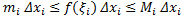
Складывая эти неравенства, получаем
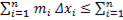
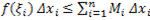. (7)
Согласно определению сумм Дарбу и интегральной суммы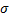 
утверждения (7) и (6) равносильны. ●
С в о й с т в о 2. Справедливы равенства
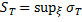, (8)
. (9)
○ Докажем утверждение (8). Согласно определению точной верхней грани нужно доказать, что выполняются следующие условия:
.
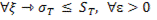
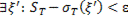Первое из этих условий выполняется в силу (6). Докажем второе условие.
Так как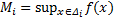 
, то по определению точной верхней грани
:
.
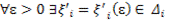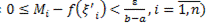Умножая -е неравенство на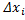 
и складывая все полученные неравенства, находим
,
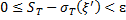Где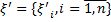 
- выборка. Итак, утверждение (8) доказано. Аналогично доказывается, что справедливо и утверждение (9).●
Следующее свойство сумм Дарбу связано с ещё одним понятием для разбиений. Назовём разбиение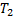 
продолжением (измельчением) разбиения 
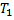, если каждая точка разбиения 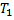является точкой разбиения 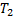. Иначе говоря, Разбиение 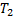либо совпадает с разбиением 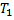, либо получено из 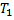добавлением по крайней мере одной новой точки.
С в о й с т в о 3. Если разбиение 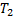- продолжение разбиения 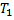, то
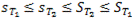(10)
т.е. при измельчении разбиения нижняя сумма Дарбу не уменьшается, а верхняя не увеличивается.
○ Для доказательства неравенств (10) достаточно рассмотреть случай, когда разбиение 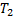получается из разбиения 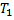добавлением только одной точки 
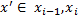. пусть 
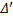и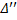 
- отрезки, на которые точка 
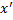разбивает отрезок 
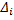, а 
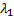и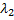 
- длины этих отрезков; тогда 
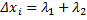. Обозначим 
, 
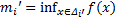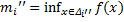. Очевидно, что 
, 
.
В суммах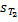 
и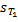 
равны все соответствующие слагаемые, за исключением тех, которые связаны с отрезком 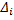. Поэтому
+
,
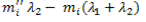где , . Следовательно,
+
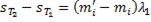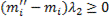, т.е. 
.
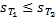Аналогично доказывается неравенство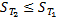 
. Отсюда, используя неравенство 
(см.(6)), получаем цепочку неравенств (10). ●
С в о й с т в о 4. Для любых разбиени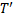й 
и 
справедливо неравенство
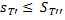(11)
○ Пусть разбиение 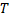является продолжением как разбиения 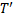, так и разбиения (в качестве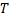 
можно взять 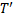и добавить к нему те точки разбиения , которые не входят в ).
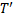Из неравенств (10) при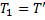 
, 
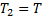получаем
.
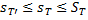Полагая в (10) 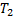= 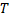и =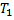
, находим
.
Объединяя полученные неравенства, имеем
,
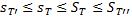Откуда следует неравенство (11).●
С в о й с т в о 5. Существуют числа
,
Удовлетворяющие для любых разбиени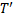й и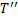 
отрезка условию
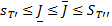(12)
Эти числа называют соответственно нижним и верхним интегралами Дарбу от функции 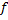на отрезке .
○ Из неравенства (11) по теореме об отделимости числовых множеств следует, что существует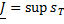 
и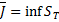 
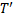(супремум и инфимум по всевозможным разбиениям отрезка и для любых разбиений и выполняется неравенство (12).●
В заключение отметим, что свойства 1-5 справедливы для любой ограниченной на отрезке функции.
Критерий интегрируемости функции.
Т е о р е м а 2. Для того, чтобы функция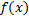 
, определённая на отрезке , была интегрируема на этом отрезке, необходимо и достаточно, чтобы эта функция была ограничена и удовлетворяла условию
<
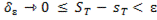. (13)
○ Н е о б х о д и м о с т ь. Пусть функция 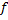интегрируема на отрезке . Тогда она ограничена (теорема 1) и в силу определения интеграла
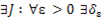>0: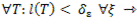
.
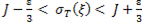Таким образом, при каждом разбиении 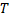отрезка , мелкость которого удовлетворяет условию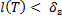 
, неравенство
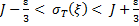(14)
Выполняется при любой выборке 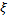. Поэтому из левого неравенства (14) и равенства (9) следует, что
. (15)
Аналогично из правого неравенства (14) и равенства (8) следует, что
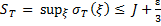. (16)
Из неравенств (15), (6) и (16) получаем цепочку неравенств
,
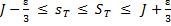откуда следует, что
.
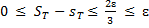Итак, интегрируемая на отрезке функция 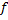удовлетворяет условию (13).
Д о с т а т о ч н о с т ь. Пусть функция 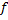ограничена на отрезке и удовлетворяет условию (13). Докажем, что функция 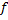интегрируема на отрезке , т.е.
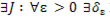>0: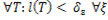
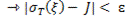. (17)
Воспользуемся свойством 5. Из неравенств (12) следует, что
,
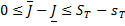откуда в силу (13) получаем неравенство
,
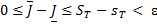Справедливое для любого разбиения 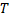такого, что 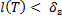. Так как числа 
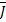и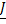 
не зависят от 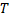, то отсюда следует, что
.
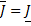Обозначим
(18)
И докажем, что число 
есть интеграл от функции 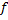на отрезке .
Из (12) и (18) следует, что
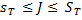, (19)
А из (19) и (6) в силу (13) получаем
.
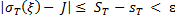Это означает, что функция интегрируема на отрезке , а число есть интеграл от на .●
