Достаточные условия локального экстремума в терминах первой и второй производной.
Теорема 5 (первое достаточное условие строгого экстремума).
Пусть функция f(x) дифференцируема в некоторой окрестности точки 
, и непрерывна в точке .
Тогда:
-
если
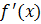меняет знак с минуса на плюс при переходе через точку , т.е. существует 
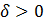такое, что
,
,
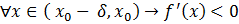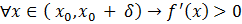то – точка строгого минимума функции f.
-
если
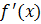меняет знак с плюса на минус при переходе через точку , то - точка строгого максимума функции f.
Пусть функция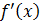 
меняет знак с минуса на плюс при переходе через точку , тогда выполняется условие а) Теоремы 5.
Если x – произвольная точка интервала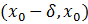 
, то функция f дифференцируема на интервале 
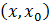и непрерывна на отрезке 
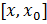. По теореме Лагранжа
,
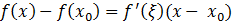где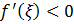 
, так как 
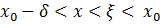и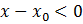 
. Отсюда следует, что
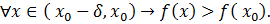
Аналогично, применяя теорему Лагранжа к функции f(x) на отрезк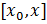е 
, где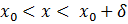
, получаем, что
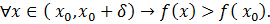
Из двух последних условий следует утверждение:
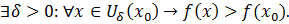
Это означает, что – точка строгого минимума функции f(x).
Аналогично рассматривается случай строгого максимума.
Замечание 3. Если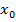 
– точка строгого экстремума функции f(x), то из этого не следует, что функция 
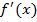меняет знак при переходе через .
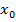Теорема 6 (второе достаточное условие строгого экстремума)
Пусть - стационарная точка функции f(x), т.е.
,
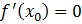И пусть существует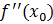 
.
Тогда:
а) если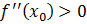 
, то – точка строгого минимума функции f(x);
б) если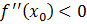 
, то – точка строгого максимума функции f(x).
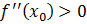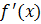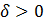Если , то по теореме о монотонности функции, функция является возрастающей в точке , т.е. существует такое, что
,
,
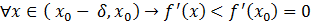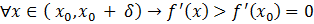откуда следует, что 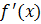меняет знак с минуса на плюс при переходе через точку. Согласно Теореме 5 точка – точка строгого минимума функции f(x). Аналогично рассматривается случай .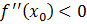
Замечание 4. Есл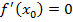и 
и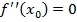 
, то в точке 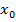функция f может иметь экстремум 
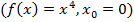, а может и не иметь 
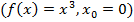. Следующая теорема дает достаточные условия экстремума для случая .
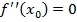Теорема 7(третье достаточное условие строгого экстремума).
Пусть существует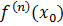 
, где n>2 и выполняются условия
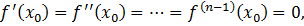
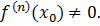
Тогда:
а) если n – четное число, то – точка экстремума функции f(x), а именно точка строгого максимума в случае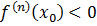 
и точка строгого минимума в случае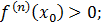
б) если n – нечетное число, то не является точкой экстремума функцииf(x).
Используя локальную формулу Тейлора для функции f(x) в окрестности точки и условия 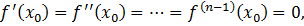получаем
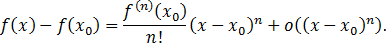
Из условия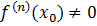 
следует, что предыдущее неравенство можно записать в виде
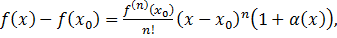(20)
Где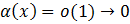 
при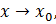 
так как 
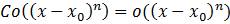при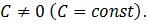
Поэтому 
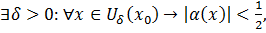откуда следует, что
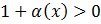для 
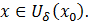(21)
Из равенства (20) в силу условия (21) получаем
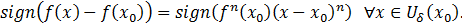(22)
а) Пусть n – четное число (n=2k), тогда
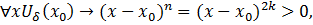
и из равенства (22) получаем
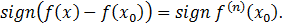
Если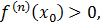 
то для 
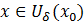выполняется неравенство
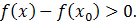
Это означает, что – точка строгого минимума функции f(x).
Аналогично, если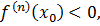 
то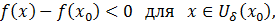 
т.е. – точка строгого максимума функции f(x).
б) Пусть n=2k+1, тогда из формулы (22) следует, что разность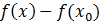 
меняет знак при переходе через точку , так как функция 
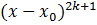меняет знак при переходе через точку . Это означает, что не является точкой экстремума функции f(x).
