Теорема 2. (Теорема Лагранжа) Пусть функция f(x)
- непрерывна на отрезке [a, b];
- дифференцируема в интервале (a, b).
Тогда существует точка с О (a, b) такая, что
| f(b) − f(a) = f '(c) · (b − a) . | (1) |
Формула (1) называется формулой Лагранжа, или формулой конечных приращений
Доказательство. Рассмотрим вспомогательную функцию
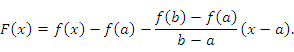
Эта функция непрерывна и дифференцируема в промежутке 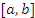 , а на его концах принимает одинаковые значения:
, а на его концах принимает одинаковые значения:
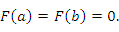
Тогда 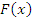 удовлетворяет всем условиям теоремы Ролля и, следовательно, существует точка
удовлетворяет всем условиям теоремы Ролля и, следовательно, существует точка 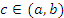 , в которой производная функции
, в которой производная функции 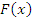 равна нулю:
равна нулю:
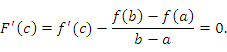
Следствие 1. В частном случае, когда 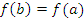 , из теоремы Лагранжа вытекает, что существует точка
, из теоремы Лагранжа вытекает, что существует точка 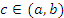 , в которой производная функции
, в которой производная функции 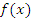 равна нулю:
равна нулю: 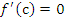 . Это означает, что теорема Лагранжа является обобщением теоремы Ролля.
. Это означает, что теорема Лагранжа является обобщением теоремы Ролля.
Следствие 2. Если 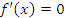 во всех точках некоторого промежутка
во всех точках некоторого промежутка 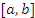 , то
, то 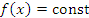 в этом промежутке.
в этом промежутке.
Действительно, пусть 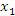 и
и 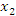 – произвольные точки промежутка
– произвольные точки промежутка 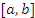 и
и 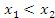 . Применяя теорему Лагранжа к промежутку
. Применяя теорему Лагранжа к промежутку 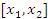 , получим
, получим
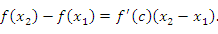
Однако 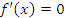 во всех точках промежутка
во всех точках промежутка 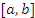 . Тогда
. Тогда
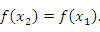
Учитывая произвольность точек 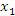 и
и 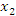 , получаем требуемое утверждение.
, получаем требуемое утверждение.
Геометрическая интерпретация теоремы Лагранжа
Представим формулу (1) в виде
|
(2) |
Число
| f(b) − f(a) |
| b − a |
есть угловой коэффициент прямой, проходящей через концы графика функции y = f(x) — точки (a, f(a) ) и (b, f(b) ), а f '(c) — угловой коэффициент касательной к этому графику в точке
(c, f(c) ). Из формулы (2) следует, что существует точка с О (a, b), в которой касательная к графику функции f(x) параллельна прямой, проходящей через концы графика (или совпадает с ней) (рис. 2).

Теорема 3. (Теорема Коши) Пусть функции f(x) и g(x)
- непрерывны на отрезке [a, b];
- дифференцируемы в интервале (a, b);
- "x О (a, b) g'(x) ≠ 0 .
Тогда существует точка c О (a, b) такая, что
|
(3) |
Формула (3) называется формулой Коши.
Доказательство. Заметим, что 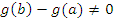 . В противном случае – согласно теореме Ролля – производная
. В противном случае – согласно теореме Ролля – производная 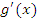 обратилась бы в нуль в некоторой точке
обратилась бы в нуль в некоторой точке 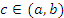 .
.
Рассмотрим вспомогательную функцию
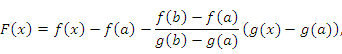
которая удовлетворяет всем условиям теоремы Ролля и, в частности, принимает одинаковые значения на концах промежутка 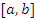 :
:
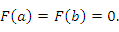
Тогда существует точка 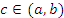 , в которой
, в которой
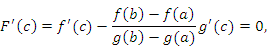
что и требовалось доказать.
Следствие. Теорема Лагранжа является частным случаем теоремы Коши при 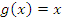 . В свою очередь теорема Ролля представляет собой частный случай теоремы Лагранжа. Таким образом, теорема Коши включает в себя в качестве частных случаев теорему Ролля и теорему Лагранжа.
. В свою очередь теорема Ролля представляет собой частный случай теоремы Лагранжа. Таким образом, теорема Коши включает в себя в качестве частных случаев теорему Ролля и теорему Лагранжа.

