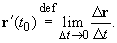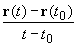 определено в соответствующей проколотой окрестности точки t0.
определено в соответствующей проколотой окрестности точки t0. Определение 3. Предел
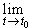
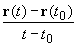 (если он, конечно, существует) называется производной векторной функции r(t) в точке t0 и обозначается r'(t0) или
(если он, конечно, существует) называется производной векторной функции r(t) в точке t0 и обозначается r'(t0) или 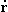 (t0)
(t0)Если положить
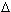 t = t - t0,
t = t - t0,  r = r(t) - r(t0) = r(t0 +
r = r(t) - r(t0) = r(t0 +  t) - r(t0), то
t) - r(t0), то
|
|
(16.17) |
Пусть r(t) = (x(t), y(t), z(t)). Так как
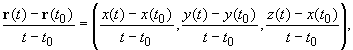
то в силу (16.9), (16.10) для того, чтобы векторная функция r(t) = (x(t), y(t), z(t)) имела производную в точке t0, необходимо и достаточно, чтобы ее координаты x(t), y(t), z(t) имели производные в точке t0, причем в этом случае
|
r'(t) = (x'(t0), y'(t0), z'(t0)). |
(16.18) |
Производную r'(t) вектор-функции r(t) называют также скоростью изменения вектора r(t) относительно параметра t. В случае когда длина вектора r(t) не меняется, производная r'(t) называется также и скоростью вращения вектора r(t), а ее абсолютная величина - численным значением скорости его вращения.
Замечание 1. По аналогии со случаем скалярных функций векторную функцию 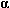 (t), t
(t), t 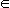 X, называют бесконечно малой по сравнению со скалярной функцией
X, называют бесконечно малой по сравнению со скалярной функцией 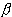 (t), t
(t), t 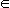 X, при t
X, при t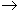 t0 и пишут
t0 и пишут 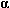 (t) = o(
(t) = o(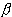 (t)), t
(t)), t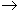 t0, если существует векторная функция
t0, если существует векторная функция  (t), определенная на том же множестве X, что и функции
(t), определенная на том же множестве X, что и функции 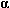 (t),
(t), 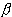 (t), такая, что в некоторой окрестности точки t = t0 имеет место равенство
(t), такая, что в некоторой окрестности точки t = t0 имеет место равенство 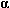 (t) =
(t) =  (t)
(t)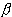 (t), t
(t), t 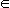 X, и
X, и
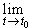
 (t) = 0.
(t) = 0.
Как и для скалярных функций, если t0 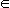 X, то функция
X, то функция  (t) непрерывна в точке t0, и потому
(t) непрерывна в точке t0, и потому  (t0) = 0.
(t0) = 0.
Замечание 2. Вектор-функция аргумента t называется линейной, если она имеет вид at + b, где a и b - какие-либо два фиксированных вектора.
После этих вводных замечаний можно определить понятие дифференцируемости и дифференциала вектор-функции