ОПРЕДЕЛЕНИЕ
Дифференциалом  функции
функции  в точке
в точке  называют главную, линейную относительно
называют главную, линейную относительно  часть ее приращения
часть ее приращения  которая равна произведению производной функции в этой точке на приращение аргумента:
которая равна произведению производной функции в этой точке на приращение аргумента:
При доказательстве правил дифференцирования будем считать функции f(x) и g(x)дифференцируемыми на некотором промежутке X.
То есть, для любого 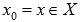 справедливо
справедливо  , где
, где 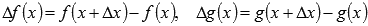 - приращения соответствующих функций.
- приращения соответствующих функций.
В другой записи  .
.
К основным правилам дифференцирования относят:

Вынесение постоянного множителя за знак производной.
Докажем формулу  . По определению производной имеем:
. По определению производной имеем:
Произвольный множитель можно выносить за знак предельного перехода (это известно из свойств предела), поэтому
На этом доказательство первого правила дифференцирования завершено.
Остальные правила дифферинцирования смотри в 3 параграфе!

