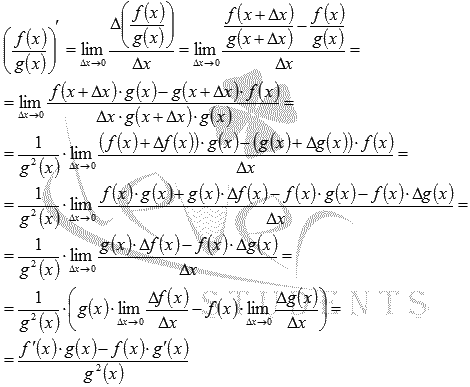При доказательстве правил дифференцирования будем считать функции f(x) и g(x)дифференцируемыми на некотором промежутке X.
То есть, для любого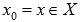 
справедливо 
, где 
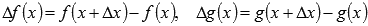- приращения соответствующих функций.
В другой записи 
.
Производная суммы
Для доказательства второго правила дифференцирования 
воспользуемся определением производной и свойством предела непрерывной функции.
Подобным образом можно доказать, что производная суммы (разности) n функций равна сумме (разности) n производных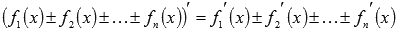 
.
Производная произведения функций
Докажем правило дифференцирования произведения двух функций 
.
Запишем предел отношения приращения произведения функций к приращению аргумента. Будем учитывать, что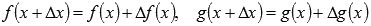 
и 
(приращение функции стремиться к нулю при приращении аргумента, стремящемся к нулю).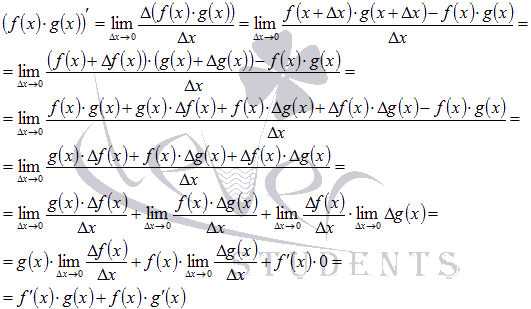
Что и требовалось доказать.
Производная частного двух функций (производная дроби).
Докажем правило дифференцирования частного двух функций (дроби)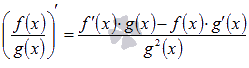 
. Стоит оговориться, что g(x) не обращается в ноль ни при каких x из промежутка X.
По определению производной
