Аналитическое задание гомотетии.
Пусть мы имеем прямоугольную декартовую систему координат Охy. Гомотетия 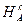 плоскости задана центром О и коэффициентом k (k ¹ 0). Согласно определению гомотетии для любой точки Х и её образа Х¢ выполняется равенство
плоскости задана центром О и коэффициентом k (k ¹ 0). Согласно определению гомотетии для любой точки Х и её образа Х¢ выполняется равенство 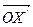 = k ×
= k × 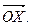
Введем координаты точек Х (x,y) и Х¢ (x¢,y¢).Тогда из предыдущего векторного равенства получим равенство для координат
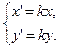 (1)
(1)
Если выбрать в качестве центра гомотетии произвольную точку
Х0 (x0,y0),
То векторное равенство несколько изменится
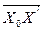 = k×
= k× 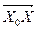 ,
,
что в координатной форме приведет нас к системе
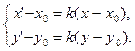 (2)
(2)
Формулы (2) представляют собой аналитическое задание гомотетии.
Таким образом формулы (1) и (2) являются формулами гомотетии плоскости с коэффициентом k и, соответственно, центрами О(0,0) и Х0 (x0,y0).
Формулы движения плоскости также нам известны:

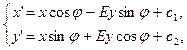 (3)
(3)
где Е = 1, если g – движение I рода, и
Е = –1, если g – движение II рода.
Поэтому, учитывая разложение подобия плоскости на движение и гомотетию, получим аналитическое выражение подобия