Введем обозначения: F1 и F2 – фокусы, разность расстояний |F2М–F1М|=2а, илиF2М–F1М=±2а.
F1F2=2с (фокусное расстояние), причем по определению 2а<2с или а<с.
Введем прямоугольную систему координат. Ось Ох проходит через точки F1 и F2, как показано на рисунке; начало координат О – середина отрезка F1F2. Тогда координаты точек: F1(–с; 0) и F2(с; 0).
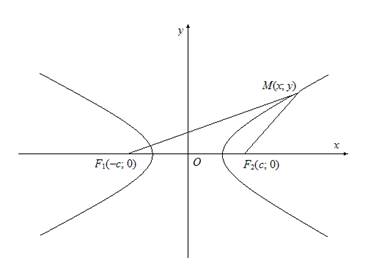
Пусть М(х; у) – произвольная точка гиперболы. Тогда по определению F2М–F1М=±2а (1).
Учитывая, что 
|F1М|= 
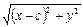и |F2М|= 
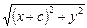, запишем это условие в координатах:
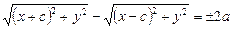. (2)
Это и есть уравнение гиперболы в выбранной системе координат. Выполним тождественные преобразования: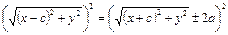 
,
,
, 
,
,
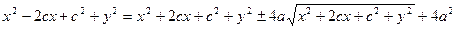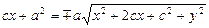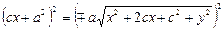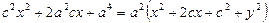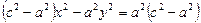. Разделим обе части равенства на (с2–а2), получим: 
.
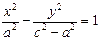По условию а<с, т.е. разность с2–а2 есть положительная величина, ее принято обозначать b2, т.е. b2=с2–а2 (3). Тогда
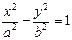(4),
Это каноническое уравнение гиперболы. Очевидно, что гипербола – линия второго порядка.
