Разверткой многогранной поверхности называется плоская фигура, получаемая последовательным совмещением всех граней поверхности с плоскостью.
Так как все грани многогранной поверхности изображаются на развертке в натуральную величину, построение ее сводится к определению величины отдельных граней поверхности – плоских многоугольников.
Существует три способа построения развертки многогранных поверхностей:
1. Способ нормального сечения;
2. Способ раскатки;
3. Способ треугольника.
Способ треугольников
Разверткой многогранника называется плоская фигура, получаемая последовательным совмещением всех граней многогранника с одной плоскостью. Так как все грани многогранника изображаются на развертке в натуральную величину, построение развертки сводится к определению натуральной величины граней – плоских многоугольников.
Способ треугольников используют для построения развертки поверхности пирамиды. Развертка боковой поверхности пирамиды - плоская фигура, состоящая из треугольников - граней пирамиды. Поэтому построение развертки поверхности пирамиды сводится к определению действительной величины ребер пирамиды и построению по трем известным сторонам треугольников - граней пирамиды.
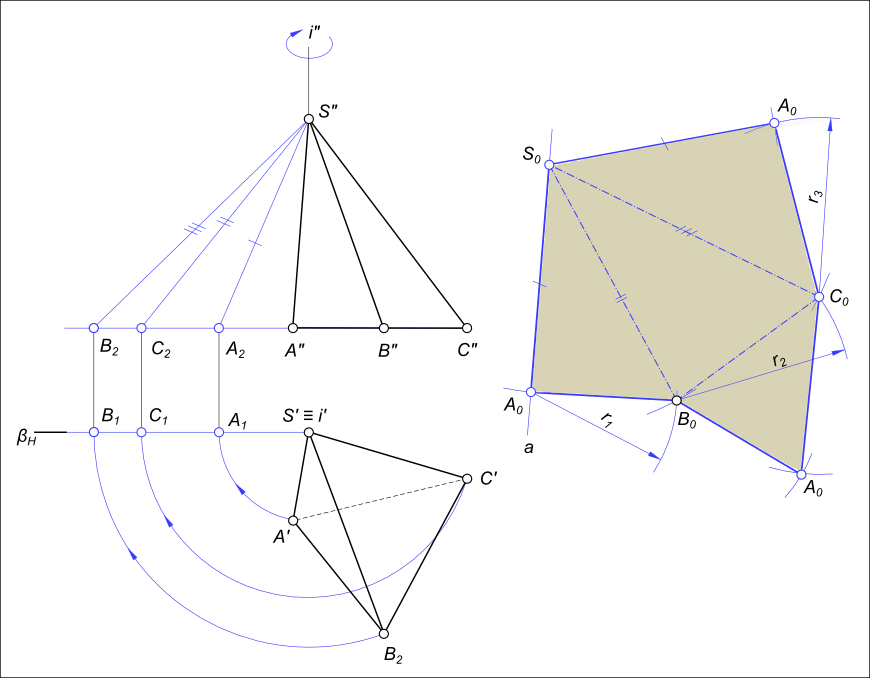
Вращаем ребра вокруг оси i (i⊥H и i∋S) и совмещаем с плоскостью β (плоскость β║V β∋i). Выполняем определение действительных величин ребер пирамиды [S"A2], [S"B2], [S"C2]. Приступая к построению развертки проводим произвольную прямую a через произвольную точку S0. Откладываем на ней от точки S0 отрезок [S0A0]≅ [S"A2]. Из точки A0 проводим дугу радиусом r1=A`B`, а из точки S0 - дугу радиусом R1=S"B2. Пересечение дуг укажет положение вершины B0ΔS0A0B0 (ΔS0A0B0≅ΔSAB - грани пирамиды). Аналогично определяем положение точек C0 и A0. Соединяя точки A0B0C0A0S0, получим развертку боковой поверхности. Присоединив к какой-либо стороне (ребру) основание (ΔABC) - получаем полную развертку поверхности пирамиды SABC.
Способ раскатки
Разверткой многогранника называется плоская фигура, получаемая последовательным совмещением всех граней многогранника с одной плоскостью. Так как все грани многогранника изображаются на развертке в натуральную величину, построение развертки сводится к определению натуральной величины граней – плоских многоугольников.
Способ раскатки используют для построения развертки призмы, в том случае, когда ее основание параллельно какой-либо одной плоскости проекции, а боковые ребра отображаются в натуральную величину на другой плоскости проекций.
Построить развертку поверхности наклонной трехгранной призмы ABCDEF, используя способ раскатки
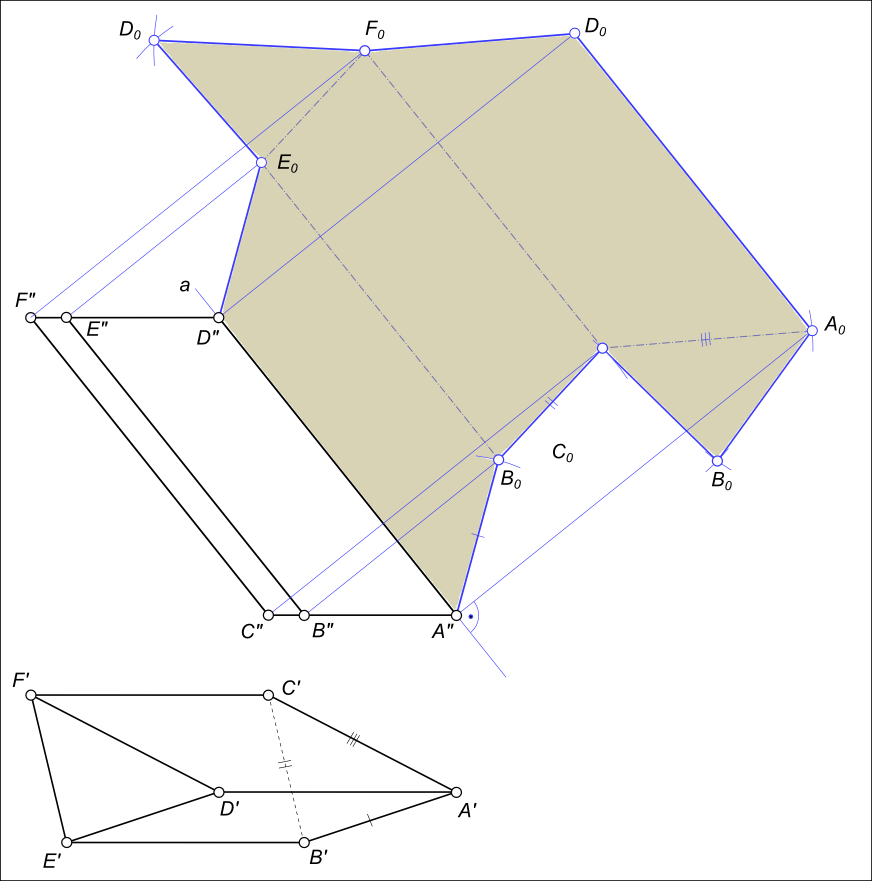
За плоскость развертки примем плоскость β, проходящую через ребро AD, параллельную фронтальной плоскости проекций. Совместим грань ADEB с плоскостью β. Для этого мысленно разрежем призму по ребру AD, и затем выполним поворот грани ADEB вокруг ребра AD. Определение совмещенного с плоскостью β положения ребра B0E0 из точки B" опускаем луч, перпендикулярный к A"D" и засекаем на нем дугой радиуса A`B`, проведенной из центра A", точку B0. Из точки B0 проводим прямую B0E0, параллельную A"D". Совмещенное положение ребра B0E0принимаем за новую ось и вращаем вокруг нее грань BEFC до совмещения с плоскостью β. Из точки C" опускаем луч, перпендикулярный к B"E", а из точки B0 - дугой окружности радиусом B`C` засекаем на нем положение точки C0. Из C0 проводим C0F0 параллельно B0E0. Аналогично определяется положение ребра A0D0. Соединив точки A"B0C0A0 и D"E0F0D0 прямыми, получим фигуру A"B0C0A0D0E0F0D" - развертку боковой поверхности призмы. Полная развертка призмы будет получена если к каким-либо из звеньев ломаных линий A"B0C0A0 и D"E0F0D0 пристроить треугольники основания A0B0C0 и D0E0F0.
Способ нормального сечения
Под разверткой многогранной поверхности подразумевают плоскую фигуру, составленную из граней этой поверхности, совмещенных с одной плоскостью. Так как все грани многогранника изображаются на развертке в натуральную величину, построение развертки сводится к определению натуральной величины граней – плоских многоугольников.
Способ нормального сечения применяется для развертки призматических гранных поверхностей. Отличительная особенность данного способа является построение сечения призмы плоскостью нормальной (перпендикулярной) по отношению к ее боковым ребрам. При последующем развертывании призмы линия нормального сечения выстраивается в прямую линию и используется для откладывания от нее натуральной величины отрезков боковых ребер.
Построить развертку наклонной трехгранной призмы ABCDEF, иcпользуя способ нормального сечения.
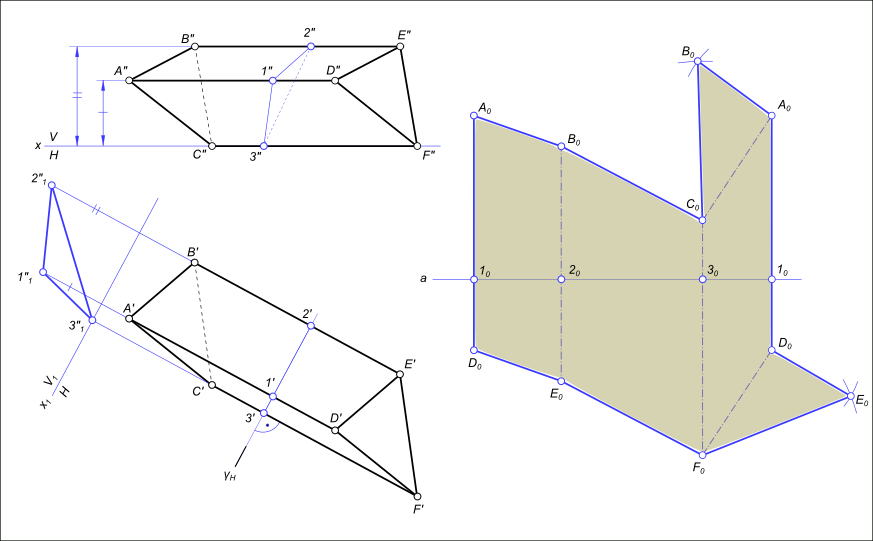
Построим сечение заданной призмы вспомогательной плоскостью γH перпендикулярной к ее боковым ребрам и горизонтальной плоскости проекций H. Методом перемены плоскостей проекций определяем действительную величину сторон Δ123. В произвольном месте эпюра проводим горизонтально прямую a. От точки 10, отмеченной на этой прямой, откладываем отрезки [1020], [2030], [3010], конгруентные сторонам Δ123. Через точки 102030 и 10 проводим прямые перпендикулярные к прямой a, и откладываем на них от точек 102030 и 10 отрезки, конгруентные соответствующим действительным величинам отрезков боковых ребер. Полученные точки A0B0C0A и D0E0 F0D0 соединяем прямыми. Ребра AD, BE, и CF параллельны плоскости H, поэтому на нее они проецируются в действительную величину. Плоская фигура A0B0C0A0D0E0F0D0 - развертка боковой поверхности призмы. К ней пристроены основания призмы ΔA0B0C0 и ΔD0E0F0.

