Метрика, диаметр.

Метрикой на множестве X называется отображение p : X x X -> R+, удовлетворяющее следующим аксиомам:

. рефлексивность: p(x; y) = 0 <-> x = y;

. симметричность: p(x; y) = p(y; x);

. неравенство треугольника: p(x; y) +p(y; z) >= p(x; z).

Метрическим пространством называется множество с определенной на нем

метрикой.

________

Аксиома обычно называется неравенством треугольника. Функцию от двух аргументов , будем называть еще метрикой пространства .

Легко видеть, что -мерное пространство с метрикой

где , является метрическим пространством.

_________

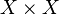Метрическое пространство есть пара $(X,;d)$ , где $X$ — множество (подлежащее множество метрического пространства, множество точекметрического пространства), а $d$ — числовая функция (метрика пространства), которая определена на декартовом произведении $Xtimes X$ и принимает значения в множестве вещественных чисел — такая, что для точек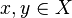 $x, y in X$

$d(x,;y)=0Leftrightarrow x=y$ (аксиома тождества).
$d(x,;y)=d(y,;x)$ (аксиома симметрии).
$d(x,;z)leqslant d(x,;y)+d(y,;z)$ (аксиома треугольника или неравенство треугольника).

Замечание: Из аксиом следует неотрицательность функции расстояния, поскольку $0=d(x,;x)leqslant d(x,;y)+d(y,;x)=2d(x,;y)$ .

______________________________________________________________________

Под диаметром метрического пространства понимается точная верхняя грань расстояний между парами его точек. В частности:
- Диаметр графа — это максимальное из расстояний между парами его вершин. Расстояние между вершинами определяется как наименьшее число рёбер, которые необходимо пройти, чтобы добраться из одной вершины в другую. Иначе говоря, это расстояние между двумя вершинами графа, максимально удаленными друг от друга.
- Диаметр геометрической фигуры — максимальное расстояние между точками этой фигуры.
- Диаметром множества $M$ , лежащего в метрическом пространстве с метрикой $rho$ , называется величина $(sup_{x,y in M}rho(x, y))$ . Например, диаметр n-размерного гиперкуба со стороной s равен

$d = scdot sqrt{n}$ .