Опера́тор Лапла́са (Лапласиан) — дифференциальный оператор, действующий в линейном пространстве гладких функций и обозначаемый символом  . Функции
. Функции  он ставит в соответствие функцию
он ставит в соответствие функцию  .
.
В произвольных ортогональных криволинейных координатах  :
:
![Delta f (q_1, q_2, q_3) = operatorname{div},operatorname{grad},f(q_1, q_2, q_3) = frac{1}{H_1H_2H_3}left[ frac{partial}{partial q_1}left( frac{H_2H_3}{H_1}frac{partial f}{partial q_1} right) + frac{partial}{partial q_2}left( frac{H_1H_3}{H_2}frac{partial f}{partial q_2} right) + frac{partial}{partial q_3}left( frac{H_1H_2}{H_3}frac{partial f}{partial q_3} right)right]](http://images.wikia.com/math/ru/images/math/d/e/b/deb602446ac5ae1d8c6c9f09c1210359.png) ,
,
где  - коэффициенты Ламе.
- коэффициенты Ламе.


или

Оператор Лапласа часто записывается следующим образом  , то есть скалярное произведение оператора набла на себя.
, то есть скалярное произведение оператора набла на себя.
Опера́тор Лапла́са (лапласиа́н, оператор дельта) — дифференциальный оператор, действующий в линейном пространстве гладких функций и обозначаемый символом  . Функции
. Функции  он ставит в соответствие функцию
он ставит в соответствие функцию  .
.
Оператор Лапласа эквивалентен последовательному взятию операций градиента и дивергенции:  , таким образом, значение оператора Лапласа в точке может быть истолковано как плотность источников (стоков) потенциального векторного поля
, таким образом, значение оператора Лапласа в точке может быть истолковано как плотность источников (стоков) потенциального векторного поля  в этой точке. В декартовой системе координат оператор Лапласа часто обозначается следующим образом
в этой точке. В декартовой системе координат оператор Лапласа часто обозначается следующим образом  , то есть в виде скалярного произведения оператора набла на себя. Оператор Лапласа унитарен.
, то есть в виде скалярного произведения оператора набла на себя. Оператор Лапласа унитарен.
________________________________________________________________________
Гармони́ческая фу́нкция — вещественная функция  , определенная и дважды непрерывно дифференцируемая на евклидовом пространстве
, определенная и дважды непрерывно дифференцируемая на евклидовом пространстве  (или его открытом подмножестве), удовлетворяющая уравнению Лапласа:
(или его открытом подмножестве), удовлетворяющая уравнению Лапласа:

где  — оператор Лапласа, то есть сумма вторых производных по всем прямоугольным декартовым координатам xi (n = dim D - размерность пространства).
— оператор Лапласа, то есть сумма вторых производных по всем прямоугольным декартовым координатам xi (n = dim D - размерность пространства).
Например, гармонической функцией является электростатический потенциал в точках, где отсутствует заряд.
Рассмотрим уравнение Лапласа на плоскости
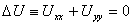 (1)
(1)
и в пространстве
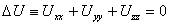 (2)
(2)
Функции U=U(x,y) на плоскости и U=U(x,y,z) в пространстве, имеющие непрерывные частные производные второго порядка и удовлетворяющие, соответственно, уравнению Лапласа (1) или (2) в некоторой области D, называются гармоническими в этой области.[1]
Простейшими примерами гармонических функций являются линейные функции: 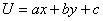 на плоскости и
на плоскости и 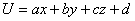 в пространстве. Особый интерес представляют решения уравнений Лапласа, обладающие сферической или цилиндрической (в случае двух независимых переменных – круговой) симметрией.
в пространстве. Особый интерес представляют решения уравнений Лапласа, обладающие сферической или цилиндрической (в случае двух независимых переменных – круговой) симметрией.
Решение 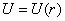 , обладающее сферической симметрией, будет определяться из обыкновенного дифференциального уравнения
, обладающее сферической симметрией, будет определяться из обыкновенного дифференциального уравнения
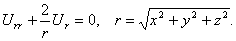
Это уравнение получится, если подставить искомую функцию в уравнение Лапласа (2), записанное в сферических координатах. Интегрируя это уравнение, находим 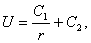 где
где 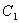 и
и 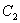 - произвольные постоянные. Полагая
- произвольные постоянные. Полагая 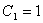 ,
, 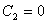 , получим функцию
, получим функцию 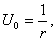 которую часто называют фундаментальным решением уравнения Лапласа в пространстве. Функция
которую часто называют фундаментальным решением уравнения Лапласа в пространстве. Функция 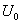 является гармонической всюду в пространстве, кроме начала координат.
является гармонической всюду в пространстве, кроме начала координат.
Аналогично, полагая 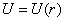 и пользуясь уравнением Лапласа в цилиндрических и полярных координатах можно найти решения, обладающие цилиндрической или круговой симметрией:
и пользуясь уравнением Лапласа в цилиндрических и полярных координатах можно найти решения, обладающие цилиндрической или круговой симметрией:
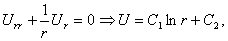 где
где 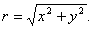
Выбирая 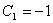 и
и 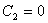 , будем иметь функцию
, будем иметь функцию 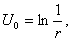 которую называют фундаментальным решением уравнения Лапласа на плоскости (в случае двух независимых переменных). Функция
которую называют фундаментальным решением уравнения Лапласа на плоскости (в случае двух независимых переменных). Функция 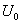 удовлетворяет уравнению Лапласа (1) всюду на плоскости, кроме начала координат, где она обращается в бесконечность. Фундаментальные решения уравнения Лапласа имеют, помимо большого значения в теории гармонических функций, важный физический смысл.
удовлетворяет уравнению Лапласа (1) всюду на плоскости, кроме начала координат, где она обращается в бесконечность. Фундаментальные решения уравнения Лапласа имеют, помимо большого значения в теории гармонических функций, важный физический смысл.
Рассмотрим в пространстве электрическое поле, образованное точечным зарядом величины 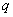 , помещенным в начало координат. Тогда потенциал этого поля равен
, помещенным в начало координат. Тогда потенциал этого поля равен 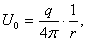 Аналогично, если рассмотреть поле, создаваемое заряженной прямой, то потенциал такого поля будет равен
Аналогично, если рассмотреть поле, создаваемое заряженной прямой, то потенциал такого поля будет равен 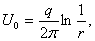 где
где 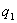 - линейная плотность заряда (то есть заряд, рассчитанный на единицу длину).
- линейная плотность заряда (то есть заряд, рассчитанный на единицу длину).
А теперь приступим к изучению некоторых свойств гармонических функций.
Теорема о среднем. Пусть функция 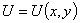 гармоническая в некотором круге
гармоническая в некотором круге 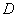 радиуса
радиуса 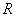 с центром
с центром 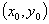 и непрерывная в соответствующем замкнутом круге
и непрерывная в соответствующем замкнутом круге 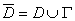 . Тогда значение этой функции в центре круга равно ее среднему значению на окружности Г, ограничивающей данный круг [14], то есть
. Тогда значение этой функции в центре круга равно ее среднему значению на окружности Г, ограничивающей данный круг [14], то есть 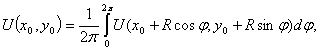 (3)
(3)
При доказательстве этой теоремы применяется интегральная формула Пуассона для круга, которая будет доказана позже. Она имеет вид
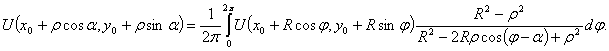
Если в этой формуле положить 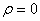 , то получится формула (3).
, то получится формула (3).
Теорему о среднем можно представить и в другой форме. Для этого запишем формулу (3) для произвольного круга радиуса 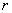 , где
, где 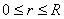
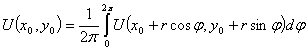 (4)
(4)
Умножив обе части равенства (4) на 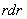 и проинтегрировав по
и проинтегрировав по 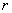 в пределах от 0 до
в пределах от 0 до 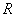 , получим:
, получим: 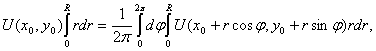 или
или
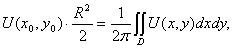 где
где 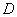 - круг радиуса
- круг радиуса 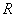 . Разделив обе части полученного равенства на
. Разделив обе части полученного равенства на 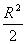 , получится
, получится 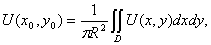 (5)
(5)
В правой части формулы (5) записано среднее значение гармонической функции U(x,y) в круге радиуса R [1].
Имеет место и обратная теорема: если в некоторой области 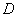 функция
функция 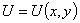 непрерывная и для каждой точки
непрерывная и для каждой точки 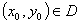 выполняется теорема о среднем в любом сколь угодно малом круге с центром в точке
выполняется теорема о среднем в любом сколь угодно малом круге с центром в точке 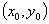 , то эта функция гармоническая в
, то эта функция гармоническая в 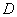 .
.

