Пусть линейный оператор A действует в линейном пространстве над полем комплексных чисел размерности n и его характеристический многочлен имеет вид
f(λ)=(λ1-λ)^m1 * (λ2-λ)^m2 * … * (λp-λ)^mp, где λj≠λk при j≠k
m1+m2+…+mp = n
Тогда в этом пространстве существует базис, состоящий из собственных и присоединенных векторов оператора A, в котором матрица оператора имеет блочно-диагональную форму (она называется жордановой формой)
A' =
([A(λ1)]
… [A(λ2)]
……….. [A(λp)])
где A(λj) — жорданов блок, соответствующий собственному значению λj.
Указанный базис называется жордановым.
Жорданову форму можно рассматривать как обобщение квадратной диагональной матрицы. На ее диагонали размещаются т.н. жордановы клетки, соответствующие собственным значениям λi исходной матрицы. Собственные числа λi могут быть равными в различных клетках. Структура жордановой матрицы может выглядеть, например, так:
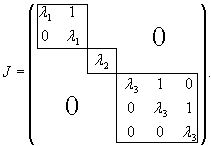
Сами собственные значения матрицы λi находятся на главной диагонали, причем каждое собственное число λi встречается столько раз, какова его алгебраическая кратность ki. В каждой клетке размером более 1 имеется параллельный ряд над главной диагональю, состоящий из единиц. Все остальные элементы жордановой матрицы равны нулю. Порядок расположения жордановых клеток в матрице определен неоднозначно.
Алгоритм нахождения нормальной жордановой формы
1. Найти собственные значения lj матрицы А и их кратности.
2. Для каждого найденного в п.1 собственного значения lj определить количество и размер жордановых клеток.
3. Записать матрицу J:
J=diag[J1(l1),..., Jp(l1), J1(l2),..., Jq(lk)]
4. Найти вектора, составляющие жорданов базис, и записать матрицу H.

