Анализируя эпюру касательных напряжений (рис.5.7) можно отметить, что наибольшие напряжения возникают на поверхности вала, в центральной части они значительно меньше и на продольной оси равны нулю. Следовательно, в сплошном валу материал, находящийся в центральной части в значительной степени недогружен, его вклад в прочность вала мал. Поэтому рациональным для валов считается кольцевое сечение.
Деформации при кручении и условие жесткости вала
Из выражения (5.5) следует, что
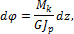
интегрируя которое по длине вала, получим:
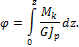
Если Мк = const и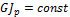 
по всей длине вала, то абсолютный угол закручивания
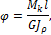
где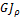 
- жесткость вала при кручении.
При скачкообразном изменении по длине бруса крутящего момента угол закручивания между его начальным и конечным сечениями определяется как сумма углов закручивания по участкам с постоянным Mk
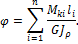
Угол закручивания, приходящийся на единицу длины, называют относительным углом закручивания
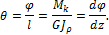
Для обеспечения требуемой жесткости вала необходимо, чтобы наибольший относительный угол закручивания не превосходил допускаемого:
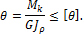
Эта формула выражает условие жесткости вала при кручении. Обычно принимается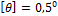 
на 1 м длины вала.
Расчеты на прочность и жесткость валов круглого и кольцевого сечений
При расчетах на прочность при кручении (также как и при растяжении) могут решаться три задачи:
а) проверочный расчет – проверить, выдержит ли вал приложенную нагрузку;
б) проектировочный расчет - определить размеры вала из условия его прочности;
в) расчет по несущей способности - определить максимально допустимый крутящий момент.
- При проверочном расчете на прочность рекомендуется следующий порядок расчета валов при кручении:
1) по схеме вала и действующим на него скручивающим моментам строят эпюру внутренних крутящих моментов по отдельным участкам;
2) выбирают материал для рассчитываемого вала и определяют для этого материала допускаемое напряжение, например по формуле (5.9),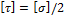 
;
3) для участка вала с максимальным по модулю значением крутящего момента записывают условие прочности при кручении
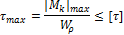
- Проектировочный расчет проводится, исходя из условия прочности на основе следующего соотношения:
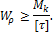
Для сплошного круглого сечения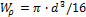 
, отсюда можем записать выражение для определения диаметра вала из условия его прочности:
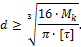
Для кольцевого сечения
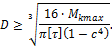
Определив размеры вала из условия прочности, проверяют вал на жесткость.
Условие жесткости требует, чтобы максимальный относительный угол закручивания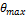 
, был меньше или в предельном случае равен допускаемому углу закручивания единицы длины вала, т.е.
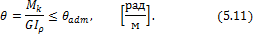
Из условия прочности можно найти необходимый для обеспечения прочности полярный момент сопротивления сечения, а по нему и диаметр вала:
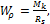но Wp = 0,2d3, поэтому
Из формулы (5.11) можно найти необходимый полярный момент инерции сечения, а по нему и диаметр вала
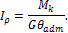
В этой формуле допускаемый относительный угол закручивания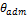 
должен быть выражен в радианах; если этот угол дан в градусах, то соотношение для определения Ip будет выглядеть следующим образом:
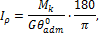
но Ip = 0,1d 4 , поэтому
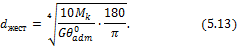
Из двух диаметров, рассчитанных по формулам (5.12) и (5.13), в качестве окончательного диаметра выбирается больший, который обычно округляется до целых миллиметров.
В случае расчета размеров вала кольцевого поперечного сечения при заданном соотношении внутреннего dвн и наружного диаметров d, т.е. при заданном параметре k = dвн /d, формулы (5.12) и (5.13) принимают вид:
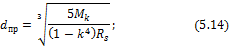
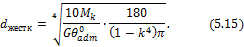
Пример 4.
Подобрать диаметр сплошного вала, передающего мощность N=450 л.с. при частоте вращения n=300 об/мин. Угол закручивания не должен превышать одного градуса на 2 метра длины вал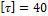а; 
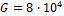МПа, 
МПа.
Решение.
Крутящий момент определяем из уравнения
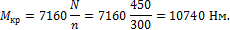
Диаметр вала по условию прочности определяется из уравнения
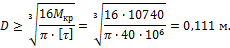
Диаметр вала по условию жесткости определяется из уравнения
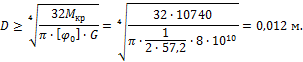
Выбираем больший размер 0,112 м.
Пример 5.
Имеются два равнопрочных вала из одного материала, одинаковой длины, передающих одинаковый крутящий момент; один из них сплошной, а другой полый с коэффициентом полости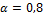 
. Во сколько раз сплошной вал тяжелее полого?
Решение.
Равнопрочными валами из одинакового материала считаются такие валы, у которых при одинаковых крутящих моментах, возникают одинаковые максимальные касательные напряжения, то есть
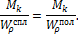
Условие равной прочности переходит в условие равенства моментов сопротивления:
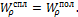
Откуда получаем:
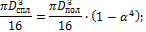
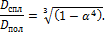
Отношение весов двух валов равно отношению площадей их поперечных сечений:
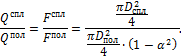
Подставляя в это уравнение отношение диаметров из условия равной прочности, получим
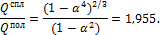
Как показывает этот результат, полый вал, будучи одинаковым по прочности, вдвое легче сплошного. Это объясняется тем, что в силу линейного закона распределения касательных напряжений по радиусу вала, внутренние слои относительно мало нагружены.
Пример 6.
Найти мощность в квт, передаваемую валом, если диаметр сплошного вала d=0,15 м, число оборотов вала в минуту n=120, модуль сдвига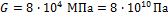 
и угол закручивания участка вала длиной 7,5 м равен 1/15 радиан.
Решение.
Из формулы
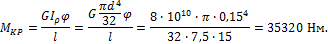
Определим передаваемую мощность
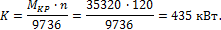
Пример 7.
Определить, на сколько процентов увеличится наибольшее напряжение вала при кручении, если в валу сделано центральное отверстие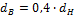 
(С=0,4).
Решение.
Полагая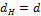 
, получим следующие выражения для напряжений сплошного и полого валов:
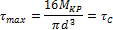
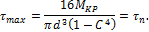
Искомая разница в напряжениях
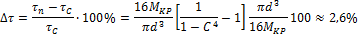
Пример 8.
Заменить сплошной вал диаметра d=300 мм полым равнопрочным валом с наружным диаметром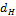 
=350 мм. Найти внутренний диаметр полого вала 
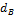и сравнить веса этих валов.
Решение.
Наибольшие касательные напряжения в обоих валах должны быть равными между собой:
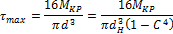
Отсюда определим коэффициент С
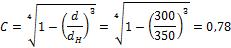
Внутренний диаметр полого вала
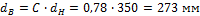
Отношение весов равно отношению площадей поперечных сечений:
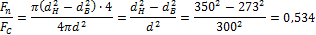
Из приведенных примеров 5 и 6 видно, что изготовление пустотелых валов, т.е. валов, у которых малонагруженная внутренняя часть удаляется, является весьма эффективным средством снижения затраты материала, а следовательно, и облегчения веса валов. При этом наибольшие напряжения, возникающие в пустотелом валу, мало отличаются от максимальных напряжений в валу сплошного сечения при том же наружном диаметре.
Так в примере 5 за счет сверления при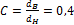 
, дающем облегчение вала на 16%, максимальные напряжения в наружных волокнах полого вала возросли всего на 2,6%. В примере 6 равнопрочный пустотелый вал, но с несколько большим наружным диаметром по сравнению со сплошным валом, оказался легче сплошного на 53,4%. Эти примеры наглядно свидетельствуют о рациональности применения пустотелых валов, что широко используется в некоторых областях современного машиностроения, в частности, в моторостроении.
Пример 9.
На участке сплошного круглого вала D=10 см действует крутящий момент Т=8 кHм. Проверить прочность и жёсткость вала, если τadm=50 МПа, Кt adm=0,5 град/м и модуль сдвига G=0,8∙105 МПа.
Решение.
Условие безопасной прочности
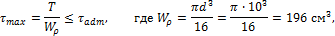
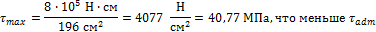
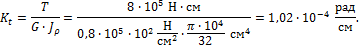
Выразив Kt в размерности град/м, получим
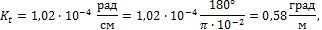
что превышает величину допускаемого отно
