размера 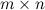 называется прямоугольная таблица специального вида, состоящая из
называется прямоугольная таблица специального вида, состоящая из 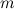 строк и
строк и 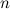 столбцов, заполненная некоторыми элементами.
столбцов, заполненная некоторыми элементами.
Количество строк и столбцов матрицы задают ее размеры.
Обозначение: 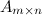
Элементы матрицы  обозначаются
обозначаются 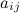 , где
, где 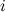 - номер строки, в которой находится элемент, а
- номер строки, в которой находится элемент, а 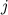 - номер столбца.
- номер столбца.
Основные понятия матрицы:
Числа m и n называются порядками матрицы. В случае, если m=n, матрица называется квадратной, а число m=n — ее порядком.
В дальнейшем для записи матрицы будут применяться обозначение:

Впрочем, для краткого обозначения матрицы часто используется одна большая буква латинского алфавита, (например, А), либо символ ||aij||, а иногда и с разъяснением: A=||aij||=(aij) (i=1,2,…,m; j=1,2,…n)
Числа aij, входящие в состав данной матрицы, называются ее элементами. В записи aij первый индекс i означает номер строки, а второй индекс j — номер столбца.
Например, матрица:
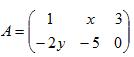
это матрица порядка 2×3, ее элементы a11=1, a12=x, a13=3, a21=-2y, …
Виды матриц:
Введем понятие матриц: квадратных, диагональных, единичных и нулевых.
1.Квадратная матрица
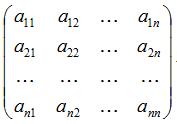
вводятся понятие главной и побочной диагоналей. Главной диагональю матрицы называется диагональ, идущая из левого верхнего угла матрицы в правый нижний ее угол.
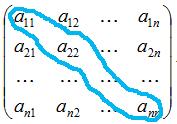
Побочной диагональю той же матрицы называется диагональ, идущая из левого нижнего угла в правый верхний угол.
2.Диагональная матрица
Диагональной называется квадратная матрица, у которой все элементы вне главной диагонали равны нулю.
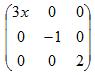
3.Понятие единочной матрицы
Единичной (обозначается Е иногда I) называется диагональная матрица с единицами на главной диагонали.

4.Нулевая матрица
Нулевой называется матрица, все элементы которой равны нулю.

5.Квадратная матрица
Две матрицы А и В называются равными (А=В), если они одинакового размера (т.е. имеют одинаковое количество строе и одинаковое количество столбцов и их соответствующие элементы равны). Так, если
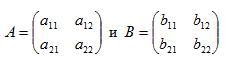
то А=B, если a11=b11, a12=b12, a21=b21, a22=b22
Действия над матрицами
1. Сложение матриц - поэлементная операция
2. Вычитание матриц - поэлементная операция
3. Произведение матрицы на число - поэлементная операция
4. Умножение A*B матриц по правилу строка на столбец (число столбцов матрицы А должно быть равно числу строк матрицы B)
Amk*Bkn=Cmn причем каждый элемент сij матрицы Cmn равен сумме произведений элементов i-ой строки матрицы А на соответствующие элемеенты j-го столбца матрицы B , т.е.
Пример:
5. Возведение в степень
m>1 целое положительное число. А - квадратная матрица (m=n) т.е. актуально только для квадратных матриц
6. Транспонирование матрицы А. Транспонированную матрицу обозначают AT или A'
Строки и столбцы поменялись местами
Пример:
{Понятие определителя n-ого порядка. Схемы вычисления определителей 2-ого и 3-его порядков. Свойства определителей}
Определитель n-го порядка
Определителем или детерминантом n-го порядка называется число записываемое в виде

и вычисляемым по данным числам  (действительным или комплексным) — элементам определителя
(действительным или комплексным) — элементам определителя
Схемы вычисления определителей 2-ого и 3-его порядков
Теорема Крамера.
Пусть (дельта)-определитель матрицы системы А,а (дельта)i-определитель матрицы,получается из матрицы А заменой j-го столбца столбцов свободных чисел.Тогда,если (дельта) не равна 0,то система имеет единственное решение,определяемое во формуле:
1.Определитель 2-го порядка вычисляется по формуле
2. Определитель третьего порядка вычисляется по формуле
Существует удобная схема для вычисления определителя третьего порядка (см. рис. 1 и рис. 2).
Свойство определителей
1.Если какая-либо строка (столбец) матрицы состоит из одних нулей,то её определитель равен 0.
2.Если все элементы какой-либо строки (столбца) матрицы умножить на чило (лямбда),то её определитель умножится на это число (лямбда).
3.При транспонировании матрицы её определитель не изменяется.
Транспонирование-в математике,это преобразование квадратной матрицы-замена столбцов на строки или наоборот.
4.При перестановки двух строк (столбцов) матрицы её определитель меняет знак на противоположный.
5.Если квадратная матрица содержит две одинаковые строки (столбца),то её определитель равен 0
6.Если элементы двух строк (столбцов)матрицы пропорциональны,то её определитель равен 0
7.Сумма произведений элементов какой-либо строки (столбца)матрицы на алгебраические дополнения элементов другой строки (столбца) этой матрицы равно 0
8.Определитель матрицы не изменяется,если к элементам какой-либо строки (столбца) матрицы прибавить элементы другой строки (столбца),предварительно умноженные на одно и то же число.
9.Сумма произведений чисел b1,b2,...,bn на алгебраические дополнение элементов любой строки (столбца) равна определителю матрицы,полученной из данной заменой элементов этой строки (столбца) b1,b2,...bn.
10.Определитель произведения двух квадратных матриц равен произведению их определителей |C|=|А|*|B|,где С=А*В;А и В-матрицы n-го порядка.
{Минор и алгебраическое дополнение элемента определителя. Теорема о разложении определителя}
Минор и алгебраическое дополнение элемента определителя
1.Минор.
Минором 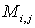 элемента
элемента 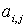 матрицы n-го порядка называется определитель матрицы (n-1)-го порядка, полученный из матрицы А вычеркиванием i-й строки и j-го столбца.
матрицы n-го порядка называется определитель матрицы (n-1)-го порядка, полученный из матрицы А вычеркиванием i-й строки и j-го столбца.
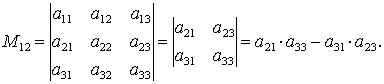
2.Алгеброическое дополнение.
Алгебраическим дополнением Аij элемента аij матрицы n-го порядка называется его минор, взятый со знаком, зависящий от номера строки и номера столбца:
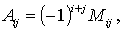
т.е. алгебраическое дополнение совпадает с минором, когда сумма номеров строки и столбца – четное число, и отличается от минора знаком, когда сумма номеров строки и столба – нечетное число.
Теорема о разложении определителя
Теорема Лапласа:
Пусть в определителе d порядка n произвольно выбраны k строк (или k столбцов), 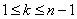 . Тогда сумма произведений всех миноров k-го порядка, содержащихся в выбранных строках, на их алгебраические дополнения равна определителю d.
. Тогда сумма произведений всех миноров k-го порядка, содержащихся в выбранных строках, на их алгебраические дополнения равна определителю d.
Для вычисления определителей в общем случае k берут равным 1. Т.е. в определителе d порядка n произвольно выбрана строка (или столбец). Тогда сумма произведений всех элементов, содержащихся в выбранной строке (или столбце), на их алгебраические дополнения равна определителю d.
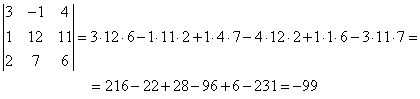
,
Знак:
«плюс, если сумма номеров всех строк и столбцов, в которых расположен минор M четна, и минус, если эта сумма нечетна.»
А минор мы взяли состоящий из одного единственного элемента 10, который стоит в первом столбце третьей строки.

Итак:
Четвертое слагаемое этой суммы равно 0, именно поэтому стоит выбирать строки или столбцы с максимальным числом нулевых элементов.
{Обратная матрица}
Обра́тная ма́трица — такая матрица A−1, при умножении на которую, исходная матрица A даёт в результате единичную матрицу E:
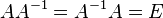
Квадратная матрица обратима тогда и только тогда, когда она невырожденная, то есть её определитель не равен нулю. Для неквадратных матриц и вырожденных матриц обратных матриц не существует. Однако возможно обобщить это понятие и ввести псевдообратные матрицы, похожие на обратные по многим свойствам.
Свойства обратной матрицы:
 , где
, где  обозначает определитель.
обозначает определитель.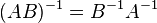 для любых двух обратимых матриц
для любых двух обратимых матриц  и
и  .
. где
где  обозначает транспонированную матрицу.
обозначает транспонированную матрицу. для любого коэффициента
для любого коэффициента  .
.- Если необходимо решить систему линейных уравнений
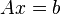 , (b — ненулевой вектор) где
, (b — ненулевой вектор) где  — искомый вектор, и если
— искомый вектор, и если 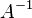 существует, то
существует, то  . В противном случае либо размерность пространства решений больше нуля, либо их нет вовсе.
. В противном случае либо размерность пространства решений больше нуля, либо их нет вовсе.
{Ранг матрицы. Преобразования матрицы, не меняющие ее ранга}
Ранг матрицы
Ранг матрицы – это максимальное количество линейно независимых строк. Или: ранг матрицы – это максимальное количество линейно независимых столбцов. Да, их количество всегда совпадает.
Сойство ранга матрицы:
1. Ранг матрицы равен нулю только для нулевой матрицы. В других случаях ранг матрицы равен некоторому положительном числу.
2. Ранг прямоугольной матрицы не превышает меньшего из двух чисел 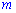 и
и 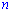 т.е.
т.е.  .
.
3. Для квадратной матрицы 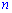 -го порядка
-го порядка 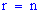 только тогда, когда матрица невырожденная.
только тогда, когда матрица невырожденная.
Невырожденная матрица (иначе неособенная матрица) ― квадратная матрица, определитель которой отличен от нуля. В противном случае матрица называется вырожденной.
4. В случае квадратной матрицы если 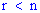 то определитель матрицы равен нулю.
то определитель матрицы равен нулю.
r-ранг-rank
n-порядок матрицы
Преобразования матрицы, не изменяющие ее ранг
Рассмотрим следующие элементарные преобразования матриц:
- Перестановка строк или столбцов.
- Умножение строки или столбца на ненулевое число.
- Прибавление к строке (столбцу) другой строки (столбца), предварительно умноженной на любое число.
Теорема. Элементарные преобразования не изменяют ранг матрицы.
Для доказательства теоремы достаточно убедиться в том, что в результате элементарных преобразований нулевой определитель остается нулевым, а ненулевой – ненулевым.
- Перестановка строк или столбцов матрицы изменяет только знак определителя.
- При умножении строки (столбца) матрицы на ненулевое число определитель умножается на это число.
- Определитель не изменяется, если к строке (столбцу) прибавляется другая строка (столбец).
{Системы m линейных уравнений с n неизвестными. Основные понятия. Матричный вид системы линейных уравнений}
Уравнение называется линейным, если оно содержит переменные только в первой степени и не содержит произведений переменных
| Правило Крамера: | ||||||||||||||||||||||||||||||||||||||||||||
|
Пусть задана система n линейных уравнений с n неизвестными
Составим из коэффициентов при неизвестных определитель и назовем его определителем системы: Решение. вычислим определитель системы:
Найдем далее вспомогательные определители:
Тогда х1=30, х2=20, х3=-60. Основные понятия Соответственно, решить систему уравнений — значит найти множество всех ее решений или доказать, что это множество пусто. Поскольку число уравнений и число неизвестных может не совпадать, возможны три случая:
Матричный вид системы линейных уравнений 1.Матричный метод применим к решению систем уравнений, где число уравнений равно числу неизвестных. В общем случае линейное уравнение имеет вид: a1x1+a2x2+...+anxn=b где:
Любой n-мерный вектор Х = (x1, x2,....xn) называется решением уравнения, если при подстановке его координат уравнение обращается в тождество. Два линейных уравнения называются равносильными, если они имеют одно и тоже множество решений. Три случая при решении линейных уравнений:
{Вектор, как геометрический объект. Коллинеарные и компланарные векторы. Координаты вектора. Длина вектора. Направляющие косинусы}Вектор – направленный отрезок. Другими словами, вектором называется отрезок, для которого указано, какой из его концов является началом, а какой концом. На рисунках направление вектора обозначается стрелкой от начала к концу. Если длина рассматриваемого отрезка равна нулю, то есть отрезок вырождается в точку, то эта точка тоже может рассматриваться как вектор. Такой вектор называется нулевым и имеет произвольное направление.
На изображены ненулевые векторы Длиной (модулем) ненулевого вектора Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Поскольку нулевой вектор может иметь произвольное направление, то разумно считать его коллинеарным любому ненулевому вектору. Если два ненулевых вектора 1.Равные вектора Два вектора называются равными, если они сонаправлены и их длины равны 2.Два вектора называются противоположными, если их длины равны, и они противоположно направлены
3.Суммой двух векторов
Отложим от произвольной точки A вектор Для сложения двух неколлинеарных векторов можно воспользоваться правилом параллелограмма.
Для любых векторов
Разностью векторов
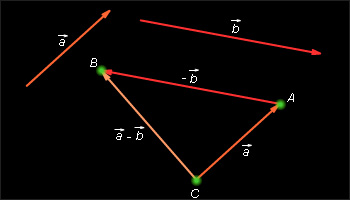
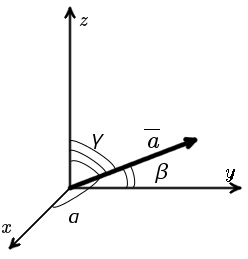
Направляющие косинуса Направляющие косинусы вектора a – это косинусы углов, которые вектор образует с положительными полуосями координат. Чтобы найти направляющие косинусы вектора a необходимо соответствующие координаты вектора поделить на модуль вектора. Свойство направляющих косинусов:
Сумма квадратов направляющих косинусов равна единице. Формулы вычисления направляющих косинусов вектора1.Формула вычисления направляющих косинусов вектора для плоских задачВ случае плоской задачи направляющие косинусы вектора a = {ax ; ay} можно найти воспользовавшись следующей формулой
Свойство: cos
2 α + cos2 β = 1
2.Формула вычисления направляющих косинусов вектора для пространственных задачВ случае пространственной задачи направляющие косинусы вектора a = {ax ; ay ; az} можно найти воспользовавшись следующей формулой
Свойство: cos2 α + cos2 β + cos2 γ = 1
{Линейные операции над векторами. Условие коллинеарности векторов, выраженное в координатах}Линейными операциями называют операции сложения и вычитания векторов и умножения вектора на число. 1.Сложение векторов. Пусть
Ту же сумму можно получить иным способом. Отложим от точки О векторы
2.Вычитание векторов. Разностью Если векторы
Т.о., если на векторах
3.Умножение вектора на число. Произведением вектора 1) 2) Очевидно, что при Построим, например, векторы
Из определения следует: два вектора Свойства линейных операций: 1) 2) 3) 4) 5) 6) 7) Условия коллинеарности векторов Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Нулевой вектор считается коллинеарным любому другому вектору. Условия коллинеарности векторов Два вектора будут коллинеарны при выполнении любого из этих условий: Условие коллинеарности векторов 1.
Два вектора a и b коллинеарны, если существует число n такое, что a = n · b Условия коллинеарности векторов 2.
Два вектора коллинеарны, если отношения их координат равны. N.B. Условие 2 неприменимо если один из компонентов вектора равен нулю. Условия коллинеарности векторов 3.
Два вектора коллинеарны, если их векторное произведение равно нулевому вектору. N.B. Условие 3 применимо только для трехмерных (пространственных) задач.
{Скалярное произведение векторов и его свойства. Условие перпендикулярности векторов. Угол между векторами}Скалярным произведением двух ненулевых векторов а и b называется число, равное произведению длин этих векторов на косинус угла междуними. Обозначается ab,а* b(или( а, b)).Итак, по определению,
Свойства скалярного произведения: 1. Скалярное произведение обладает переместительным свойством: ab=ba
5. Если векторы а и b (ненулевые) взаимно перпендикулярны, то их скалярное произведение равно нулю, т. е. если a ^b, то ab=0. Справедливо и обратное утверждение: если ab=0 и а¹ 0 ¹b, то а ^ b . Условия перпендикулярности векторов Два ненулевых вектора называются перпендикулярными, если угол между ними равен девяноста градусам ( Теорема:Для перпендикулярности двух ненулевых векторов Угол между векторами Углом между двумя векторами, отложенными от одной точки, называется кратчайший угол, на который нужно повернуть один из векторов вокруг своего начала до положения сонаправленности с другим вектором.
Основное соотношение.
Косинус угла между векторами равен скалярному произведению векторов, поделенному на произведение модулей векторов. Формула вычисления угла между векторами:
{Векторное произведение и его свойства}Определение: Три некомпланарных вектора a, b и с, взятые в указанном порядке, образуют правую тройку, если с конца третьего вектора с кратчайший поворот от первого вектора а ко второму вектору b виден совершающимся против часовой стрелки, и левую, если по часовой.
Векторным произведением вектора а на вектор b называется вектор с, который: 1. Перпендикулярен векторам a и b, т. е. с^а и с^b; 2. Имеет длину, численно равную площади параллелограмма, построенного на векторах а и b как на сторонах (см. рис. 17), т. е. 3.Векторы a, b и с образуют правую тройку.
Векторное произведение обозначается а х b или [а,b]. Из определения векторного произведения непосредственно вытекают следующие соотношения между ортами i , j и k (рис.18) Свойства векторного произведения: 1. При перестановке сомножителей векторное произведение меняет знак, т.е. а хb =(b хa ) (см. рис. 19). Векторы ахb и b ха коллинеарны, имеют одинаковые модули (площадь параллелограмма остается неизменной), но противоположно направлены (тройки а , b , а хb и a , b , bxa противоположной ориентации). Стало быть axb = -(bxa ). 2. Векторное произведение обладает сочетательным свойством относительно скалярного множителя, т. е. l(а хb ) = (lа ) х b = а х (lb ). 3. Два ненулевых вектора а и b коллинеарны тогда и только тогда, когда их векторное произведение равно нулевому вектору, т. е. а||b <=>ахb =0. 4. Векторное произведение обладает распределительным свойством: (a+b) хс= ахс+b хс.
{Общее уравнение прямой на плоскости. Случаи расположения прямой относительно осей координат. Уравнение прямой в отрезках}Прямая (прямая линия) - это бесконечная линия, по которой проходит кратчайший путь между любыми двумя её точками.
Уравнение прямой на плоскостиЛюбую прямую на плоскости можно задать уравнением прямой первой степени вида A x + B y + C = 0
где A и B не могут быть одновременно равны нулю. Уравнение прямой с угловым коэффициентомОбщее уравнение прямой при B≠0 можно привести к виду y = k x + b
где k- угловой коэффициент равный тангенсу угла, образованного данной прямой и положительным направлением оси ОХ Уравнение прямой в отрезках на осяхЕсли прямая пересекает оси OX и OY в точках с координатами (a, 0) и (0, b), то она может быть найдена используя формулу уравнения прямой в отрезках
Уравнение прямой, проходящей через две различные точки на плоскостиЕсли прямая проходит через две точки A(x1, y1) и B(x2, y2), такие что x1 ≠ x2 и y1 ≠ y2 то уравнение прямойможно найти, используя следующую формулу
|
 |
x
=
l t
+
x
0 |
|
y
=
m t
+
y
0 |
где (x0, y0) - координаты точки лежащей на прямой, {l, m} - координаты направляющего вектора прямой.
Каноническое уравнение прямой на плоскости
Если известны координаты точки A(x0, y0) лежащей на прямой и направляющего вектора n = {l; m}, то уравнение прямой можно записать в каноническом виде, используя следующую формулу
|
x
-
x
0 |
= |
y
-
y
0 |
|
l
|
m
|
Случаи расположения прямой относительно осей координат
Как расположена прямая относительно осей координат, если ее уравнение ax + by + c = 0 имеет тот или иной частный вид?
1. Если a = 0, b ≠ 0, то прямая параллельна оси x.
2. Если b = 0, a ≠ 0, то прямая параллельна оси y.
3. Если c = 0, то прямая проходит через начало координат.
Уравнение прямой в отрезках
Уравнение прямой в отрезках на плоскости в прямоугольной системе координат Oxy имеет вид  , где a и b - некоторые отличные от нуля действительные числа.
, где a и b - некоторые отличные от нуля действительные числа.

{Уравнение прямой с угловым коэффициентом. Уравнение прямой, проходящей через данную точку в данном направлении. Уравнение прямой, проходящей через две данные точки}
Угол наклона прямой к оси Ox в фиксированной прямоугольной декартовой системе координат Oxy на плоскости - это угол, отсчитываемый от положительного направления оси Ох до прямой против хода часовой стрелки.
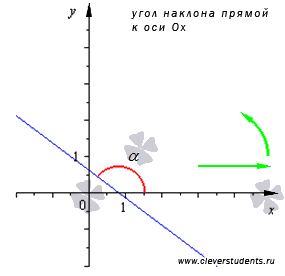
Если прямая параллельна оси абсцисс или совпадает с ней, то угол ее наклона считают равным нулю. Таким образом, угол наклона прямой  может принимать значения из интервала
может принимать значения из интервала  .
.
Угловым коэффициентом прямой называется тангенс угла наклона этой прямой.
Угловой коэффициент прямой обычно обозначают буквой k. Тогда по определению 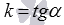 .
.
Положительный угловой коэффициент прямой указывает на возрастание ее графика функции, отрицательный угловой коэффициент – на убывание. Этой теме посвящена статья нахождение промежутков возрастания и убывания функции.
На рисунке показан угол наклона прямой и указано значение углового коэффициента при различных вариантах расположения прямой относительно прямоугольной системы координат.

{Уравнение прямой, проходящей через данную точку в данном направлении}
Предположим, что прямая проходит через точку M1 (x1,y1) и образует с осью OX угол j. Составим уравнение этой прямой.
 Y
Y
Будем искать уравнение прямой в виде уравнения с угловым коэффициентом: y = k · x + b. Угловой коэффициент прямой можно найти, зная угол наклона k = tg j. Возьмем произвольную точку M (x, y), лежащую на этой прямой, и найдем уравнение, связывающее переменные x и y. Так как точки М и M1 лежат на прямой, то их координаты удовлетворяют уравнению прямой:
y = k · x + b,
y1 = k · x1 + b.
Вычитая эти равенства, получим:
y - y1 = k · (x - x1) - уравнение прямой, проходящей через данную точку в данном направлении.
Уравнение прямой, проходящей через две данные точки
Пусть даны точки A(x1;y1) и B(x2;y2). Уравнение прямой, проходящей через точки A(x1;y1) и B(x2;y2) имеет вид:
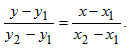
Решение: Подставляя в уравнение (8) x1=1, y1=2, x2=-1; y2=1 получим: 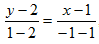 откуда
откуда 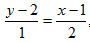 или 2у-4=х-1, или окончательно х-2у+3=0
или 2у-4=х-1, или окончательно х-2у+3=0
.











 т.е. система совместна.
т.е. система совместна.



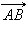
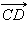
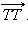
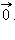
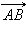
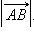
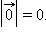
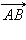
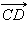
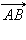
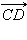
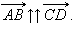
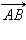
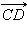
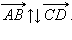
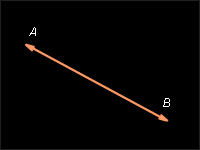
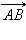
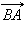
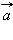
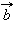
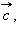
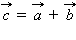
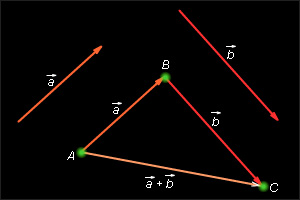
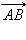 , равный
, равный 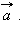 Теперь от точки B отложим вектор
Теперь от точки B отложим вектор 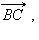 равный
равный 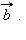 Вектор
Вектор  и называется суммой векторов
и называется суммой векторов 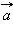 и
и 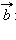
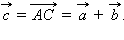 Это правило сложения векторов называется правилом треугольника.
Это правило сложения векторов называется правилом треугольника.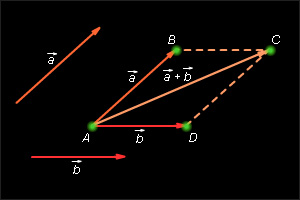
 и
и 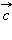 справедливы равенства:
справедливы равенства: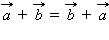 (переместительный закон);
(переместительный закон);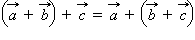 (сочетательный закон).
(сочетательный закон).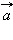
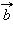
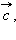
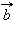
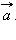
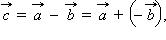

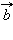 .
.



















 ,
, при
при  и
и  при
при  .
.
 .
. и
и  для заданного вектора
для заданного вектора 

 ;
; ;
; ;
;  ;
; ;
; ;
; ;
; ;
;  ;
;













