1.Основные определения переменного тока: частота, амплитуда, начальная фаза, сдвиг фаз.2.Переходный процесс при отключении катушки индуктивности от источника постоянного тока.

1.

Ток, периодически меняющийся по величине и направлению, называется переменным током. Представление о переменном токе можно получить, если медленно вращать ручку действующей модели генератора, подключенного к гальванометру. Отклонение стрелки гальванометра то вправо, то влево говорит о периодическом изменении величины и направления тока в цепи, т. е. о переменном токе.

Переменный ток, используемый в производстве и быту, изменяется по синусоидальному закону:

i = I_m sinω t   ,

где i - значение переменного тока в любой момент времени, называемое мгновенным значением переменного тока. Величина I_m, стоящая перед знаком синуса, называется амплитудой переменного тока.

Действующим значением переменного тока называется постоянный ток, который за время одного периода оказывает такое тепловое (механическое и др.) действие, как и данный переменный ток. Действующее значение для данного переменного тока есть величина постоянная и равная амплитудному значению, деленному на √2, т. е.

IД =	Im
	√2

Все определения и соотношения действующего значения переменного тока справедливы и для переменного напряжения.

Амперметр и вольтметр, работа которых основана на тепловом или механическом действии, при измерении переменного тока и напряжения показывают их действующие значения.

 

1. Мгновенное  значение - величина тока соответствующая данному моменту времени

 

2. Амплитуда - это наибольшее положительное или отрицательное значение переменного тока. Величина ω, стоящая под знаком синуса, является угловой скоростью. Произведение угловой скорости на время (ωt) представляет собой угол, возрастающий со временем.

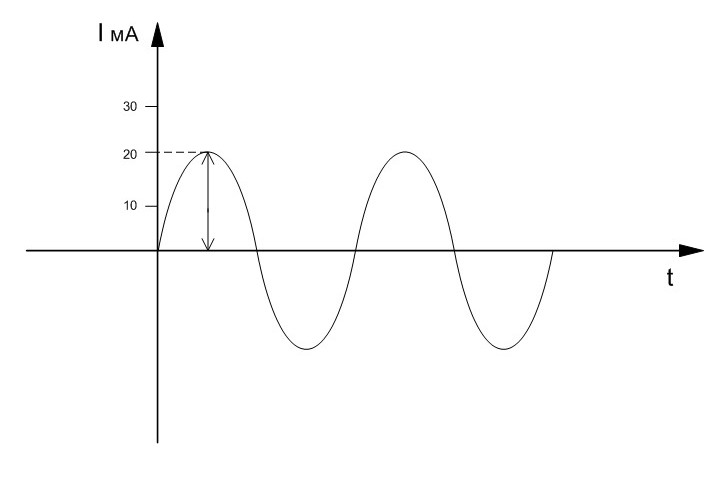
Графиком переменного тока является синусоида (см. рис.).

График переменного тока

 

 

 Амплитуда - максимальное мгновенное значение ( наибольшее значение, которого достигает переменный ток).

 

 

 

 

 

 

Здесь амплитуда 20 мА

 

 

 

 

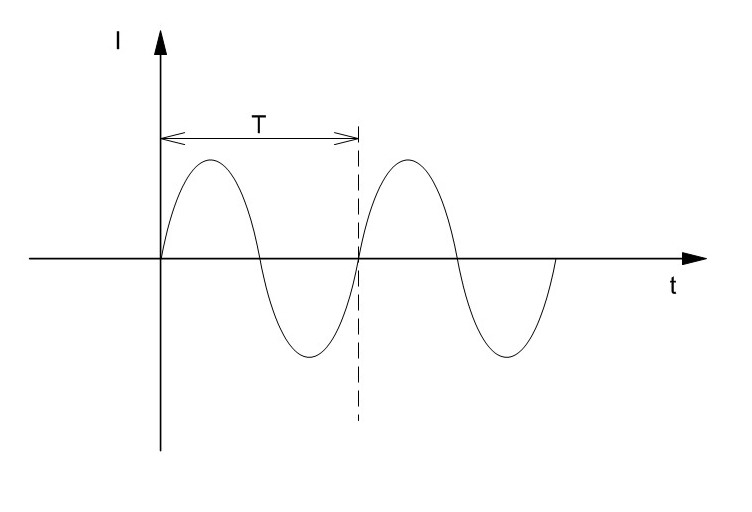
3. Периодом (T) называется время, в течение которого происходит полное изменение (колебание) тока в проводнике.

Обозначается буквой Т 

 

 

 

 

 

 

 

 

 

 

 

 

 

За один период совершается одно колебание переменного тока, т. е. период это время одного колебания. Одно колебание состоит из двух движений тока.

4.

Частотой (f) называется величина, выражающаяся числом полных колебаний тока за одну секунду. Частота измеряется в герцах (Гц). При частоте в 1 Гц происходит одно полное колебание тока за одну секунду.

Стандартной частотой переменного тока в СССР является частота 50 Гц, что соответствует 50 полным колебаниям тока за одну секунду.

Частота - величина, обратная периоду. Следовательно,

f = 1/T или T = 1/f

Переменный ток, как и постоянный, оказывает тепловое, механическое, магнитное и химическое действия. В формулы расчета теплового, механического, магнитного и химического действий переменного тока подставляется действующее значение переменного тока.

 

 

5. Фаза - это состояние переменного тока за определенный период времени

 

 

 

 

 

 

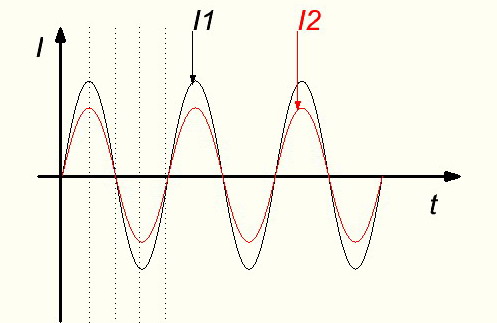
  Переменные величины могут совпадать по фазе. Это значит что они одновременно достигают нулевых значений и одновременно достигают максимальных значений одинаковых направлений.

Здесь токи I1 и I2  совпадают по фазе

 

 

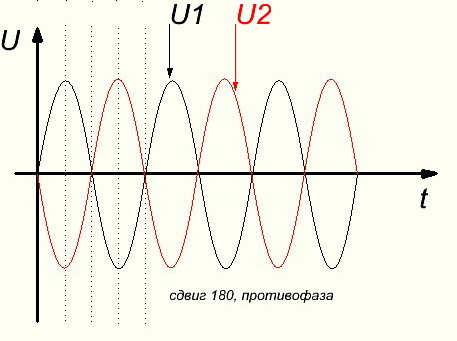
Здесь напряжения U1 и U2 находятся в противофазе.

Это значит что они одновременно достигают нулевых и максимальных значений противоположных направлений.

 

 

 

 

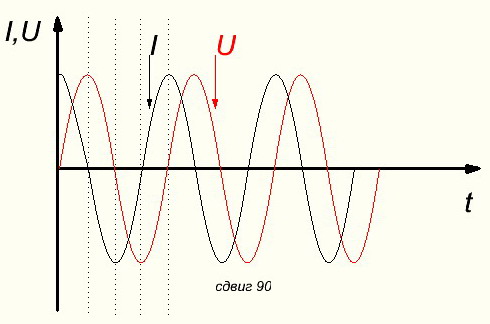
Если переменные величины не совпадают по фазе, то говорят что они сдвинуты по фазе.Сдвиг по фазе выражается в градусах или в долях периода. Весь период 360⁰ , так как период получается за один полный оборот  проводника по окружности в магнитном поле.

 

 

 

Здесь напряжение отстает от тока на 90⁰ , т. е . ток и напряжение  сдвинуты по фазе на 90⁰ .

Действительно в начале ток уже достиг максимума, а напряжение находится на нуле. Напряжение достигнет максимума через 90⁰ .

Сдвиг по фазе обозначается греческой буквой φ например  φ=90⁰ .

 

2.

Допустим, что до отключения в цепи рис. 4.5, а был установившийся ток I = U/r и энергия магнитного поля катушки составляла

Казалось бы, после размыкания выключателя ток должен мгновенно прекратиться. Однако на основании первого закона коммутации при t = 0+ ток сохраняет свое прежнее значение.

Рис. 4.5. Отключение цепи r, L(а) от сети постоянного тока; без разрядного резистора (а), с разрядным резистором (б); зависимости   i(t)  (в)  и  uL(t)(г)  при  отключении   цепи  r,   L с  разрядным резистором

Возникает как будто несоответствие: цепь разомкнута, ток есть. В действительности при размыкании выключатели происходит следующее. Ток уменьшается, и в катушке индуктируется значительная ЭДС. При этом напряжение между контактами выключателя, равное сумме напряжения сети и ЭДС самоиндукции, пробивает воздушный промежуток между контактами — возникает электрическая дуга и электрическая цепь оказывается замкнутой. По мере увеличения расстояния между контактами сопротивление дуги возрастает, ток и ЭДС уменьшаются и цепь оказывается разомкнутой. За время переходного процесса энергия магнитного поля катушки выделяется в виде теплоты в электрической дуге и сопротивлении катушки.

Переходный процесс в этом случае получается довольно сложным вследствие того, что сопротивление дуги нелинейное и изменяется во времени.

Отключение цепи с индуктивностью вызывает обгорание контактов размыкающего устройства и появление значительных ЭДС и напряжения на выводах катушки, превышающих в несколько раз напряжение сети (это может привести к пробою изоляции катушки).

Во избежание этого в силовых цепях, обладающих значительной индуктивностью (обмотки возбуждения генераторов и двигателей постоянного тока, синхронных двигателей, магнитных плит и т. п.), параллельно обмоткам включают разрядные резисторы (рис. 4.5, б).

В этом случае после отключения выключателя катушка индуктивности (r, L) оказывается замкнутой на разрядное сопротивление rр . Ток в цепи будет убывать значительно медленнее. По этой причине значение возникающей ЭДС будет существенно меньше, чем без разрядного резистора, и возникшая слабая дуга исчезает почти мгновенно. В последующих рассуждениях и выводах предполагается, что дуга между контактами не возникает и цепь размыкается мгновенно.

Уравнение цепи, составленное по второму закону Кирхгофа, имеет вид

Заменив e в (4.29), получим

Решением дифференциального уравнения будет выражение

Из характеристического уравнения pL+ (r + rp)= 0 определяют показатель степени р:

р  = -	r + rp	= -	1	.
	L		Т

Подставив это выражение в (4.31), получим

где Т = L/(r + rp) — постоянная времени цепи.

Значение А определяют из начальных условий на основании первого закона коммутации: приt = 0+

Выражение тока в цепи имеет вид

Подставив   в   (4.29)   значение   i   из   (4.32),   получим   ЭДС

е =	U	(r + rp)e-t/T = Iнач(r + rp)e-t/T.
	r

Напряжение на  выводах  катушки  равно  напряжению  на разрядном резисторе:

uк = irр =	U	rpe-t/T - Iнач rpe-t/T.
	r

В начальный момент при t = 0+

а

Из выражений (4.33) и (4.34) вытекает, что начальные значения eнач и uк.нач зависят от сопротивления разрядного резистора. При больших значениях rр они могут оказаться чрезмерно большими и опасными для изоляция установки.

На рис. 4.5, в изображены графики i(t) и uк(t) катушки после отключения цепи для двух значений rр, rр > r'р.

На практике обычно выбирают rр в 4—8 раз больше собственного сопротивления обмотки индуктивной катушки: