1.Цепь синусоидального тока с реальной катушкой индуктивности.2.Переходный процесс при зарядке конденсатора через резистор.

1.

 

Вокруг всякого проводника с током образуется магнитное поле, которое характеризуется вектором магнитной индукции В и магнитным потоком Ф:

.

Если поле образуют несколько (w) проводников с одинаковым током, то используют понятие потокосцепления ψ

(2.7)

ψ = w Ф.

Отношение потокосцепления к току, который его создает называют индуктивностью катушки

(2.8)

L = ψ / i.

При изменении во времени потокосцепления согласно закону Фарадея возникает ЭДС самоиндукции

e_L = - dψ / dt.

С учетом соотношения (2.8) для eL получаем

(2.9)

e_L = - L · di / dt.

Эта ЭДС всегда препятствует изменению тока (закон Ленца). Поэтому, чтобы через проводники все время тек ток, необходимо к проводникам прикладывать компенсирующее напряжение

(2.10)

u_L = -e_L.

Сопоставляя уравнения (2.9) и (2.10) получаем

(2.11)

u_L = L · di / dt

Это соотношение является аналогом закона Ома для индуктивности. Конструктивно индуктивность выполняется в виде катушки с проводом.

Условное обозначение индуктивности

Катушка с проводом кроме свойства создавать магнитное поле обладает активным сопротивлением R.

Условное обозначение реальной индуктивности.

Единицей измерения индуктивности является Генри (Гн). Часто используют дробные единицы

1 мкГн = 10^–6 Гн; 1 мкГн = 10^–3 Гн.

 

Реальная катушка, кроме индуктивного сопротивления, всегда обладает активным сопротивлением, которое иногда называется сопротивлением потерь. Поэтому используют схему замещения катушки, чаще всего последовательную (рис. 3.19).

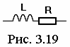
Любая катушка индуктивности обладает кроме индуктивного сопротивления еще некоторым и активным сопротивлением. При постоянном токе активное сопро­тивление катушки определяется лишь одним сопротивле­нием проволоки, которой она намотана, но при перемен­ном токе появляются потери энергии в изоляционных материалах и в магнитном сердечнике (если таковой имеется в катушке), которые проявляют себя в увеличении актив­ного, не вносящего сдвига фаз сопротивления. Кроме того, в связи с поверхностным эффектом увеличивается сопротивление самого провода катушки. В результате общее активное сопротивление катушки возрастает, и тем больше, чем выше частота тока.

Активное сопротивление R катушки можно считать включенным последовательно с индуктивным сопротивле­нием X_L (рис. 3-11). Однако при этом сопротивления R и Х L нельзя складывать арифметически, ибо они имеют различный характер: R не вызывает, а XL вызы­вает сдвиг фаз между током и падающими на них напря­жениями U_R и U_L  для на­хождения действительного сопротивления необходимо складывать их геометрически.

На основании свойства прямоугольного треугольника находят Z по формуле

        (3-26)

 

2.

Под переходным (динамическим, нестационарным) процессом или режимом в электрических цепях понимается процесс перехода цепи из одного установившегося состояния (режима) в другое. При установившихся, или стационарных, режимах в цепях постоянного тока напряжения и токи неизменны во времени, а в цепях переменного тока они представляют собой периодические функции времени. Установившиеся режимы при заданных и неизменных параметрах цепи полностью определяются только источником энергии. Следовательно, источники постоянного напряжения (или тока) создают в цепи постоянный ток, а источники переменного напряжения (или тока) – переменный ток той же частоты, что и частота источника энергии.

Переходные процессы возникают при любых изменениях режима электрической цепи: при подключении и отключении цепи, при изменении нагрузки, при возникновении аварийных режимов (короткое замыкание, обрыв провода и т.д.). Изменения в электрической цепи можно представить в виде тех или иных переключений, называемых в общем случае коммутацией. Физически переходные процессы представляют собой процессы перехода от энергетического состояния, соответствующего до коммутационному режиму, к энергетическому состоянию, соответствующему после коммутационному режиму.

Переходные процессы обычно быстро протекающие: длительность их составляет десятые, сотые, а иногда и миллиардные доли секунды. Сравнительно редко длительность переходных процессов достигает секунд и десятков секунд. Тем не менее изучение переходных процессов весьма важно, так как позволяет установить, как деформируется по форме и амплитуде сигнал, выявить превышения напряжения на отдельных участках цепи, которые могут оказаться опасными для изоляции установки, увеличения амплитуд токов, которые могут в десятки раз превышать амплитуду тока установившегося периодического процесса, а также определять продолжительность переходного процесса. С другой стороны, работа многих электротехнических устройств, особенно устройств промышленной электроники, основана на переходных процессах. Например, в электрических нагревательных печах качество выпускаемого материала зависит от характера протекания переходного процесса. Чрезмерно быстрое нагревание может стать причиной брака, а чрезмерно медленное отрицательно оказывается на качестве материала и приводит к снижению производительности.

 

как зяряжается конденсатор

 

Заряд и разряд конденсатора. Конденсатор представляет собой устройство, способное накапливать электрические заряды. Простейшим конденсатором являются две металлические пластины (электроды), разделенные каким-либо диэлектриком. Конденсатор 2 можно зарядить, если соединить его электроды с источником 1 электрической энергии постоянного тока (рис. 181, а).

При заряде конденсатора свободные электроны, имеющиеся на одном из его электродов, устремляются к положительному полюсу источника, вследствие чего этот электрод становится положительно заряженным. Электроны с отрицательного полюса источника устремляются ко второму электроду и создают на нем избыток электронов, поэтому он становится отрицательно заряженным. В результате протекания зарядного тока i3 на обоих электродах конденсатора образуются равные, но противоположные по знаку заряды и между ними возникает электрическое поле, создающее между электродами конденсатора определенную разность потенциалов. Когда эта разность потенциалов станет равной напряжению источника тока, движение электронов в цепи конденсатора, т. е. прохождение по ней тока i3 прекращается. Этот момент соответствует окончанию процесса заряда конденсатора.

При отключении от источника (рис. 181,б) конденсатор способен длительное время сохранять накопленные электрические заряды. Заряженный конденсатор является источником электрической энергии, имеющим некоторую э. д. с. ес. Если соединить электроды заряженного конденсатора каким-либо проводником (рис. 181, в), то конденсатор начнет разряжаться. При этом по цепи пойдет ток iр разряда конденсатора. Начнет уменьшаться и разность потенциалов между электродами, т. е. конденсатор будет отдавать накопленную электрическую энергию во внешнюю цепь. В тот момент, когда количество свободных электронов на каждом электроде конденсатора станет одинаковым, электрическое поле между электродами исчезнет и ток станет равным нулю. Это означает, что произошел полный разряд конденсатора, т. е. он отдал накопленную им электрическую энергию.

Включение цепи с резистором и конденсатором на постоянное напряжение (заряд конденсатора)

Если изменения тока настолько медленны, что за время установления электрического равновесия в цепи относительные изменения токов и ЭДС малы, то мгновенные значения токов и ЭДС будут подчиняться всем законам постоянного тока.

Такие токи называются медленно меняющимися, или квазистационарными. В качестве примера квазистационарных токов рассмотрим процессы зарядки и разрядки конденсатора (рис. 4.6).

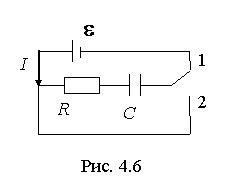
Пусть конденсатор с емкостью С включен в схему, приведенную на рисунке. Тогда, ставя переключатель в положение 1, будем заряжать конденсатор от источника тока, а перебрасывая в положение 2, - разряжать конденсатор.

Рассмотрим процесс зарядки конденсатора. Обозначим через 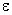 ЭДС источника, через R - сопротивление цепи (включая и внутреннее сопротивление источника) и выберем положительное направление тока, как показано на рисунке. Применим к контуру  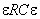второе правило Кирхгофа:

 ,

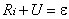где i - мгновенное значение силы тока; U - мгновенное значение напряжения на конденсаторе. Напряжение и ток выражаем, соответственно, 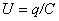, , 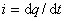где q - заряд конденсатора. Исключив из трех написанных уравнений q и i, получаем

.

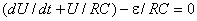Введем в дифференциальное уравнение новую переменную :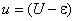

.

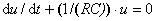В этом уравнении переменные разделяются, и в результате интегрирования находим

.

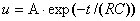Постоянную интегрирования А определим из начальных условий: при t = 0,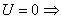  
.
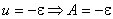
Следовательно, 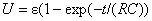. Зависимость зарядного тока от времени имеет вид

.

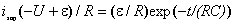Сила тока имеет наибольшее значение в начальный момент времени и асимптотически стремится к нулю в процессе зарядки.

При разрядке конденсатора исходные уравнения имеют вид

; ; .

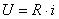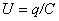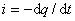В выражение для тока входит знак "минус", так как выбранное положительное направление тока соответствует уменьшению заряда конденсатора. Исключая из написанных равенств q и i, получим

.

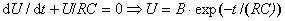Если начало отсчета времени совпадает с началом процесса разрядки, то начальные условия будут: t = 0, 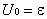. В этом случае постоянная интегрирования  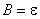и зависимость напряжения от времени имеет вид

.

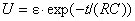Полученные результаты показывают, что процессы разрядки и зарядки конденсатора происходят не мгновенно. Для рассматриваемого контура, содержащего сопротивление и емкость, быстрота установления зависит от произведения 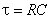, которое имеет размерность времени и называется постоянной времени данного контура. Постоянная времени показывает, через какое время после выключения ЭДС напряжение уменьшается в е раз.

 

 

 

Из схемы, приведенной на рис. 5.10, следует, что установившаяся составляющая напряжения на конденсаторе u_Cу = U, а свободная составляющая, очевидно, равна

Рис. 5.10

u_Cсв = A e^-t/τ, τ = RC.

Полагаем, что до замыкания ключа конденсатор не был заряжен (Uс(0_-) = 0). На основании законов коммутации u_C(0_-) = u_C(0₊) = 0, при t = 0; следовательно:

u_C(0) = u_Cу(0) + u_Cсв(0) или 0 = U + A, откуда А = -U.

Тогда переходное напряжение на конденсаторе

u_C = U (1 - e^-t/τ),

а переходный ток в цепи

.

Зависимости напряжений и токов от времени показаны на рис. 5.10. Из них видно, что напряжение на конденсаторе возрастает по экспоненциальному закону от нуля до напряжения источника, а ток уменьшается от начального значения до нуля также по экспоненте. Длительность их изменения определяется постоянной времени τ = RC. Здесь как и в п. 5.5.1 время переходного процесса принимается равным t ≈ (3 ÷ 5)τ.

 

.