Закон Джо́уля — Ле́нца — физический закон, дающий количественную оценку теплового действия электрического тока. Установлен в 1841 году Джеймсом Джоулем и независимо от него в 1842 году Эмилием Ленцем[1].
В словесной формулировке звучит следующим образом[2]
Мощность тепла, выделяемого в единице объёма среды при протекании электрического тока, пропорциональна произведению плотности электрического тока на величину напряженности электрического поля
Математически может быть выражен в следующей форме:
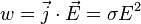
где 
— мощность выделения тепла в единице объёма, 
— плотность электрического тока, 
— напряжённость электрического поля, σ — проводимость среды.
Работа и мощность тока. Закон Джоуля-Ленца.
Прохождение электрического тока по проводнику представляет собой процесс упорядоченного движения зарядов в электрическом поле, существующем в проводнике. При этом силы электрического поля, действующие на заряды, совершают работу. Назовем эту работу “работой тока” (Aэл.) и рассчитаем ее на участке цепи 1-2, содержащем сопротивление R (см. рисунок).
Из электростатики известно, что Aэл. = q*(f1 - f2).
В темах 1 и 2 раздела “постоянный ток” показано, что
q = I*t; U = I*R; U = f1 - f2
где
t - время прохождения тока, q - заряд, прошедший от точки с потенциалом f1 до точки с потенциалом f2.
Следовательно, работу тока можно вычислить с помощью следующего соотношения:
Aэл. = I*U*t = I2*R*t = U2*t/R . (12)
Мощностью (Nэл.) называется работа, совершаемая током за единицу времени:
Nэл. = Aэл./t .
Следовательно,
Nэл. = I*U = I2*R = U2/R . (13)
Мощность электрического тока на опыте определяется с помощью амперметра и вольтметра или специального прибора – ваттметра.
Закон Джоуля-Ленца
Если по активному сопротивлению (проводнику) течет постоянный ток, то работа тока на этом участке идет на преобразование электрической энергии во внутреннюю. Увеличение внутренней энергии проводника приводит к повышению его температуры (проводник нагревается).
По закону сохранения энергии количество теплоты (Q), выделяющееся в проводнике при прохождении электрического тока, равно работе тока: Q = Aэл.
Следовательно,
Q = I*U*t = I2*R*t = U2*t/R . (14)
Формула (14) есть закон Джоуля-Ленца для однородного участка цепи.
Закон также может быть сформулирован в интегральной форме для случая протекания токов в тонких проводах[3]:
Закон Джоуля Ленца определяет выделенное количество тепла на участке электрической цепи обладающей конечным сопротивлением при прохождении тока через нее. Обязательным условием является тот факт, что на этом участке цепи должны отсутствовать химические превращения.
Возьмём проводник, к концам которого приложено напряжение. Следовательно, через него протекает ток. Таким образом, электростатическое поле и внешние силы совершают работу по перемещению электрического заряда от одного конца проводника к другому.
Если при этом проводник остается неподвижный и внутри него не происходят химические превращения. То вся работа, затрачиваемая внешними силами электростатического поля, идет на увеличение внутренней энергии проводника. То есть на его разогрев.
Данное соотношение независимо друг от друга получили два ученых. Это были Дж. Джоуль и Э.Х.Ленц. Таким образом, в итоге закон получил название закон Джоуля-Ленца.
Также можно рассматривать не весь проводник целиком, а лишь какой-то его фрагмент. Допустим если взять элементарный объём цилиндрической формы. При этом ось этого цилиндра совпадает с направлением тока. То количество тепла, которое выделяется в единицу времени в этом элементарном объёме, будет называться удельной тепловой мощностью.
В дифференциальной форме закон Джоуля Ленца будет выглядеть так
Звучит он, таким образом, удельная мощность тока будет равняться скалярному произведению векторов напряжённости эклектического поля на плотность тока в проводнике.
Также необходимо заметить, что закон Джоуля Ленца в дифференциальной форме может применяться не только к проводникам, но и к полупроводникам, а еще и к электролитам. Еще можно заметить, при этом не важна природа внешних сил, которые вызывают ток.
Примеров использования в повседневной жизни закона Джоуля Ленца можно привести массу. Например, нихромовая спираль в электрическом обогревателе. Также обычная лампочка накаливания. Либо электрическая дуга в электродуговой сварке. Так, казалось бы, на первый взгляд для совершенно несвязанных между собой вещей в основе лежит один и тот же физический процесс.
