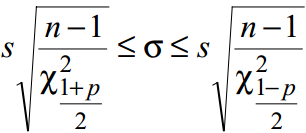Пусть количественный признак X генеральной совокупности распределен нормально и требуется оценить неизвестное генеральное среднее квадратическое отклонение s по исправленному выборочному среднему квадратическому отклонению s. Найдем доверительные интервалы, покрывающие параметр s с заданной надежностью 
.
Потребуем, чтобы выполнялось соотношение:
или 
.
Преобразуем двойное неравенство 
в равносильное неравенство 
и обозначим d/s=q. Имеем:
(A)
и необходимо найти q. С этой целью введем в рассмотрение случайную величину 
.
Оказывается, величина 
распределена по закону 
с n–1 степенями свободы. Плотность распределения c имеет вид:
Это распределение не зависит от оцениваемого параметра s, а зависит только от объема выборки n.
Преобразуем неравенство (A) так, чтобы оно приняло вид 
. Вероятность этого неравенства равна заданной вероятности 
, т.е. 
.
Предполагая, что q<1, перепишем (A) в виде:
,
далее, умножим все члены неравенства на 
:
или 
.
Вероятность того, что это неравенство, а также равносильное ему неравенство (A) будет справедливо, равна:
.
Из этого уравнения можно по заданным 
найти 
, используя имеющиеся расчетные таблицы. Вычислив по выборке 
и найдя по таблице 
, получим искомый интервал (A1), покрывающий s с заданной надежностью 
.
______
Доверительный интервал – предельные значения статистической величины, которая с заданной доверительной вероятностью γ будет находится в этом интервале при выборке большего объема. Обозначается как P(θ - ε < x < θ + ε) = γ. Мерой доверия оценке θ считается вероятность γ того, что погрешность оценки |θ - x| не превысит заданной точности ε: 
. На практике выбирают доверительную вероятность γ из достаточно близких к единице значений γ = 0.9, γ = 0.95, γ = 0.99.
- Доверительный интервал для среднеквадратического отклонения;
