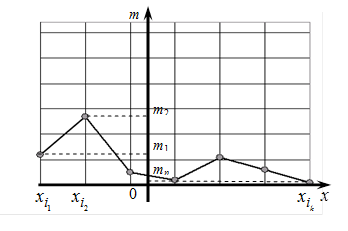
Если на плоскости построить точки (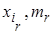 
), 
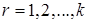, и соединить их отрезками прямых, то полученная ломанная называется полигоном абсолютных частот:
Если x - непрерывная случайная величина, то весь диапазон ее значений делят на k интервалов (длины которых определяют по формуле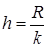 
, 
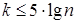) и подсчитывают количество 
, 
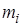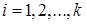, вариант, попавших в данный интервал. По абсолютным частотам каждого из интервалов находят относительные частоты 
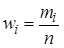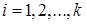, . Очевидно, 
.
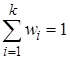Полученные интервалы и соответствующие относительные частоты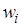 
записывают в виде таблицы, называемой интервальным статистическим рядом распределения (интервальной статистической таблицей):
| x |  |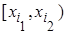
 |
… |  |
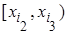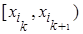| w |  |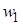
 |
… |  |
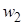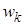Графическим представлением интервального статистического ряда является гистограмма:
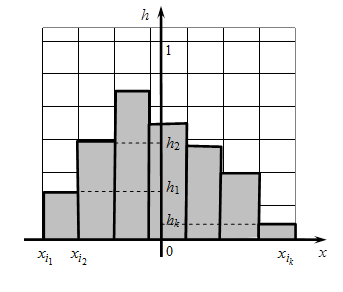
Для ее построения по оси абсцисс откладывают интервалы и на каждом из них строят прямоугольники высотой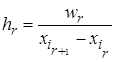 
, 
.
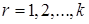Площадь гистограммы равна 1. В теории вероятностей гистограмме соответствует график плотности распределения вероятностей.
Замечание. На основании гистограммы можно построить полигон частот. Для этого достаточно соединить середины верхних сторон прямоугольников отрезками прямых. В этом случае непрерывную случайную величину можно рассматривать как дискретную, эмпирические значения которой совпадают с координатами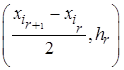 
, .
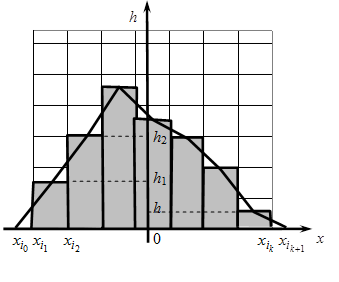
Гистограмму и полигон частот используют для подбора модели распределения изучаемой случайной величины x.
