Норма́льное распределе́ние, также называемое распределением Гаусса или Гаусса — Лапласа — распределение вероятностей, которое в одномерном случае задаётся функцией плотности вероятности, совпадающей с функцией Гаусса:
где параметр μ — математическое ожидание (среднее значение), медиана и мода распределения, а параметр σ — среднеквадратическое отклонение (σ ² — дисперсия) распределения.
Таким образом, одномерное нормальное распределение является двухпараметрическим семейством распределений.
Стандартным нормальным распределением называется нормальное распределение с математическим ожиданием μ = 0 и стандартным отклонением σ = 1.
График плотности нормального распределения называют нормальной кривой Гаусса.
Проведем исследование функции:
методами дифференциального исчисления.
-
Очевидно, что функция определена на всей оси
. -
При всех значениях
функция принимает положительные значения, т.е. нормальная кривая расположена над осью 
. -
Ось
служит горизонтальной асимптотой графика, поскольку 
. Других асимптот у графика нет. -
При
функция имеет максимум, равный 
. -
Функция четная: ее график симметричен относительно прямой
. -
Асимметрия – это свойство распределения выборки, которое характеризует несимметричность распределения случайной величины. На практике симметричные распределения встречаются редко и чтобы выявить и оценить степень асимметрии, вводят следующую меру (третий центральный момент)
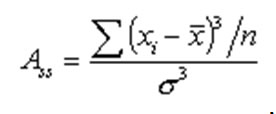, (4)
Асимметрия бывает положительной и отрицательной (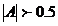
-асимметрия считается значительной
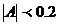- асимметрия считается незначительной). Положительная сдвигается влево, а отрицательная – вправо.
Симметричным называется распределение, в котором частоты любых двух вариантов, равностоящих в обе стороны от центра распределения, равны между собой.
Асимметрия – это свойство распределения выборки, которое характеризует несимметричность распределения случайной величины. На практике симметричные распределения встречаются редко и чтобы выявить и оценить степень асимметрии, вводят следующую меру (третий центральный момент)
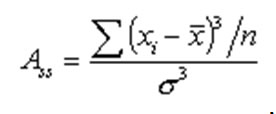, (4)
Асимметрия бывает положительной и отрицательной (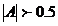 -асимметрия считается значительной
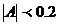- асимметрия считается незначительной). Положительная сдвигается влево, а отрицательная – вправо.
Симметричным называется распределение, в котором частоты любых двух вариантов, равностоящих в обе стороны от центра распределения, равны между собой.
