Дифференциальная функция распределения (плотность вероятности)
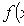
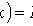
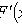
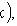
где F(x) - интегральная функция.
Свойства:
1) 
;
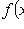
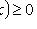2) 
;
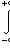
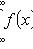
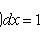3) 
;
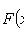
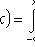
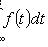В практически интересных случаях Д. ф. распределения определена для всех 
, за исключением, быть может, конечного множества точек (в которых не существует производная 
).
С помощью Д. ф. распределения можно вычислить 
, т. е. вероятность того, что случайная величина 
примет значение в 
, именно
. (**)
Последняя формула имеет следующий геометрический смысл: вероятность того, что случайная величина примет значение в , численно равна площади криволинейной трапеции, ограниченной осью абсцисс, графиком 
и прямыми 
, 
.
