Рассмотрим n взаимно независимых случайных величин X1, X2, …,Xn, которые имеют одинаковые распределения, а следовательно, и одинаковые характеристики (математическое ожидание, дисперсию и др.). Наибольший интерес представляет изучение числовых характеристик среднего арифметического этих величин.
Обозначим среднее арифметическое рассматриваемых случайных величин через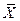 
:
.
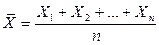Следующие ниже три положения устанавливают связь между числовыми характеристиками среднего арифметического 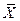и соответствующими характеристиками каждой отдельной величины.
1. Математическое ожидание среднего арифметического одинаково распределенных взаимно независимых случайных величин равно математическому ожиданию а каждой из величин:
.
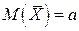Доказательство. Пользуясь свойствами математического ожидания (постоянный множитель можно вынести за знак математического ожидания; математическое ожидание суммы равно сумме математических ожиданий слагаемых), имеем
.
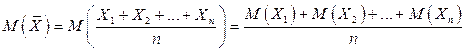Приняв во внимание, что математическое ожидание каждой из величин по условию равно а, получим
.
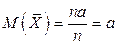2. Дисперсия среднего арифметического n одинаково распределенных взаимно независимых случайных величин в n раз меньше дисперсии D каждой из величин:
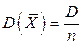. (7.3)
Доказательство. Пользуясь свойствами дисперсии (постоянный множитель можно вынести за знак дисперсии, возведя его в квадрат; дисперсия суммы независимых величин равна сумме дисперсий слагаемых), имеем
.
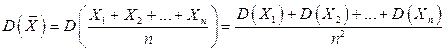Приняв во внимание, что дисперсия каждой из величин по условию равна D, получим
.
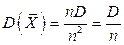3. Среднее квадратическое отклонение среднего арифметического n одинаково распределенных взаимно независимых случайных величин в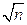 
раз меньше среднего квадратического отклонения а каждой из величин:
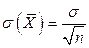. (7.4)
Доказательство. Так как 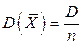, то среднее квадратическое отклонение 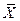равно
.
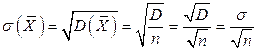