12. Локальная предельная теорема Лапласса. Интегральная Теорема Лапласса. Теорема Пуассона.

Локальная теорема Лапласа.

Если вероятность 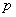 появления случайного события  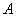в каждом испытании постоянна, то вероятность  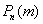того, что в  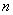испытаниях событие  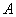наступит ровно  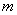раз, приближённо равна:
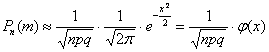 , где .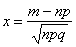

При этом, чем больше 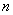, тем рассчитанная вероятность  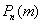будет лучше приближать точное значению 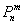, полученное (хотя бы гипотетически) по формуле Бернулли. Рекомендуемое минимальное количество  испытаний – примерно 50-100, в противном случае результат  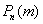может оказаться далёким от истины. Кроме того, локальная теорема Лапласа работает тем лучше, чем вероятность  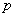ближе к 0,5, и наоборот – даёт существенную погрешность при значениях 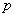, близких к нулю либо единице. По этой причине ещё одним критерием эффективного использования формулы  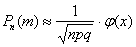является выполнение неравенства  ().

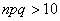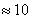Интегральная теорема Лапласа

Если вероятность 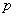 появления случайного события  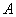в каждом испытании постоянна, то вероятность  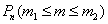того, что в  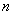испытаниях событие  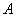наступит не менее  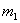и не более  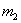раз (от  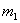до 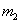 раз включительно), приближённо равна:

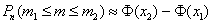, где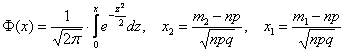 

При этом количество испытаний, разумеется, тоже должно быть достаточно большими вероятность 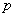 не слишком мала/велика (ориентировочно 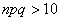), иначе приближение будет неважным либо плохим. 

Функция 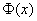называется функцией Лапласа, и её значения опять же сведены в стандартную таблицу.

Теорема Пуассона.

При больших количествах испытаний  чаще всего используют формулу Пуассона. Эта формула определяется теоремой Пуассона.

Теорема. Если вероятность  наступления события  в каждом испытании постоянна и мала, а число независимых испытаний  достаточно велико, то вероятность наступления события  ровно  раз приближенно равна

,(3.4)

где .

Доказательство. Пусть даны вероятность наступления события  в одном испытании  и число независимых испытаний . Обозначим .

Откуда . Подставим это выражение в формулу Бернулли:

При достаточно большом !!n,, и сравнительно небольшом !!m,, все скобки, за исключением предпоследней, можно принять равными единице, т.е.

Учитывая то, что  достаточно велико, правую часть этого выражения можно рассмотреть при , т.е. найти предел

Тогда получим

(3.5)