Сложение матриц
Складывать можно только матрицы одинакового размера.
Сложение матриц 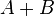 есть операция нахождения матрицы
есть операция нахождения матрицы  , все элементы которой равны попарной сумме всех соответствующих элементов матриц
, все элементы которой равны попарной сумме всех соответствующих элементов матриц  и
и  , то есть каждый элемент матрицы
, то есть каждый элемент матрицы  равен
равен

Свойства сложения матриц:
- 1.коммутативность: A+B = B+A;
- 2.ассоциативность: (A+B)+C =A+(B+C);
- 3.сложение с нулевой матрицей: A + Θ = A;
- 4.существование противоположной матрицы: A + (-A) = Θ;
Умножение матрицы на число
Умножение матрицы  на число
на число  заключается в построении матрицы
заключается в построении матрицы  .
.
Свойства умножения матриц на число:
- 1. 1A = A;
- 2. (λβ)A = λ(βA)
- 3. (λ+β)A = λA + βA
- 4. λ(A+B) = λA + λB
Произведение матриц
Умножение матриц (обозначение:  , реже со знаком умножения
, реже со знаком умножения 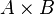 ) — есть операция вычисления матрицы
) — есть операция вычисления матрицы  , каждый элемент которой равен сумме произведений элементов в соответствующей строке первого множителя и столбце второго.
, каждый элемент которой равен сумме произведений элементов в соответствующей строке первого множителя и столбце второго.
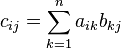
Количество столбцов в матрице  должно совпадать с количеством строк в матрице
должно совпадать с количеством строк в матрице  , иными словами, матрица
, иными словами, матрица  обязана быть согласованной с матрицей
обязана быть согласованной с матрицей  . Если матрица
. Если матрица  имеет размерность
имеет размерность  ,
,  —
— 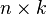 , то размерность их произведения
, то размерность их произведения  есть
есть  .
.
Свойства умножения матриц:
- 1.ассоциативность (AB)C = A(BC);
- 2.некоммутативность (в общем случае): AB
 BA;
BA;
- 3.произведение коммутативно в случае умножения с единичной матрицей: AI = IA;
- 4.дистрибутивность: (A+B)C = AC + BC, A(B+C) = AB + AC;
- 5.ассоциативность и коммутативность относительно умножения на число: (λA)B = λ(AB) = A(λB);

