Если в трехмерном пространстве задана прямоугольная система координат Oxyz, то уравнением плоскости в этой системе координат трехмерного пространства называют такое уравнение с тремя неизвестными x, y и z, которому удовлетворяют координаты всех точек плоскости и не удовлетворяют координаты никаких других точек.
Теорема
Всякое уравнение вида 
, где A, B, C и D – некоторые действительные числа, причем А, В и C одновременно не равны нулю, определяет плоскость в заданной прямоугольной системе координат Oxyz в трехмерном пространстве, и всякая плоскость в прямоугольной системе координат Oxyz в трехмерном пространстве определяется уравнением вида при некотором наборе чисел A, B, C и D.
Доказательство
Так как числа А, В и С одновременно не равны нулю, то существует точка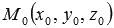 
, координаты которой удовлетворяют уравнению , то есть, справедливо равенство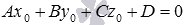 
. Отнимем левую и правую части полученного равенства соответственно от левой и правой частей уравнения , при этом получим уравнение вида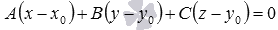 
эквивалентное исходному уравнению . Теперь, если мы докажем, что уравнение 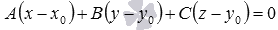определяет плоскость, то этим будет доказано, что эквивалентное ему уравнение также определяет плоскость в заданной прямоугольной системе координат в трехмерном пространстве.
Равенство 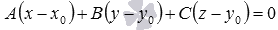представляет собой необходимое и достаточное условие перпендикулярности векторов 
и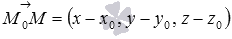 
. Иными словами, координаты плавающей точки 
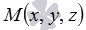удовлетворяют уравнению 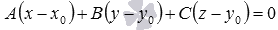тогда и только тогда, когда перпендикулярны векторы и 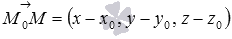. Тогда, учитывая факт, приведенный перед теоремой, мы можем утверждать, что если справедливо равенство 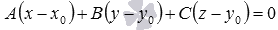, то множество точек 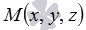определяет плоскость, нормальным вектором которой является , причем эта плоскость проходит через точку 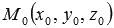. Другими словами, уравнение 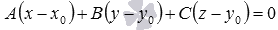определяет в прямоугольной системе координатOxyz в трехмерном пространстве указанную выше плоскость. Следовательно, эквивалентное уравнение определяет эту же плоскость. Первая часть теоремы доказана.
Приступим к доказательству второй части.
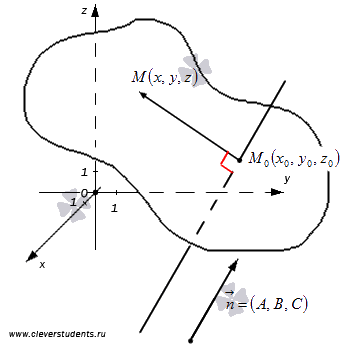
Пусть нам дана плоскость, проходящая через точку 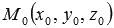, нормальным вектором которой является . Докажем, что в прямоугольной системе координат Oxyz ее задает уравнение вида .
Для этого, возьмем произвольную точку этой плоскости. Пусть этой точкой будет 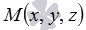. Тогда векторы и 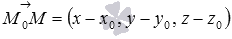будут перпендикулярны, следовательно, их скалярное произведение будет равно нулю: 
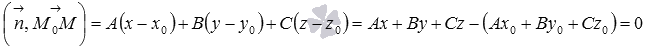. Приняв 
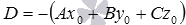, уравнение примет вид . Это уравнение и задает нашу плоскость. Итак, теорема полностью доказана.
